О причинах расхождения результатов расчета и эксперимента при определении границ устойчивости обращенных стабилизируемых маятников (по материалам статьи D.J. Acheson, T. Mullin в журнале Nature)

В.А. Грибков, Я.Д. Гордин

Инженерный журнал: наука и инновации

# 2·2017

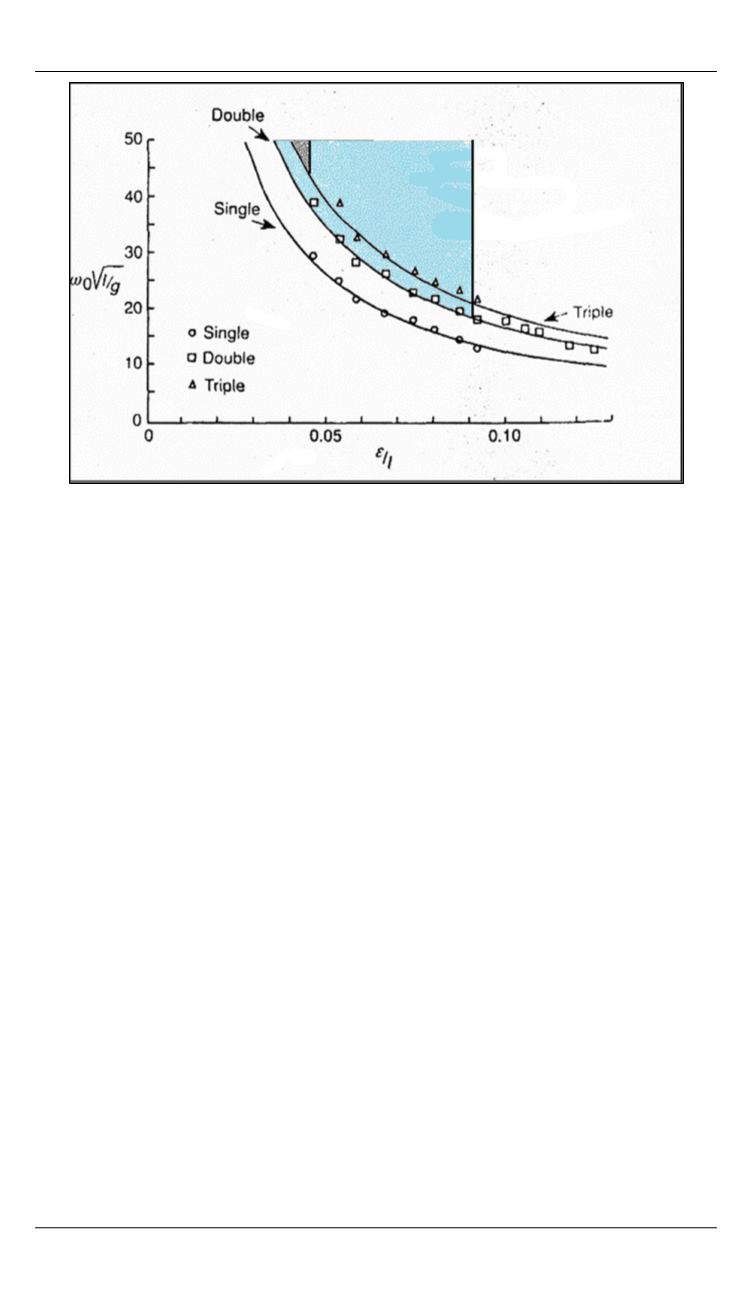
Рис. 2

. Области устойчивости двойного и тройного обращенных маятников,

рассчитанные по результатам D.J. Acheson, T. Mullin

Оказывается, что все экспериментальные значения для квазиста-

тической границы области устойчивости тройного маятника лежат на

диаграмме за пределами расчетной области устойчивости, т. е. там,

где система неустойчива. Для двойного маятника результаты лучше,

но и для него примерно половина экспериментальных данных выхо-

дит за пределы расчетной области устойчивости.

Как отмечают авторы статьи [1], несмотря на выход в эксперимен-

те за пределы области устойчивости, не удалось наблюдать режим ди-

намической неустойчивости и, соответственно, получить эксперимен-

тальные результаты для динамической границы области устойчивости

ни для одного из трех маятников. Перехода динамической границы не

зафиксировано. Предсказанный теорией ожидаемый результат (дина-

мическая неустойчивость при переходе динамической границы) не

был получен, хотя положение динамической граничной линии опреде-

лено по маятниковой теореме D.J. Acheson. Таким образом, можно

утверждать, что экспериментальные результаты D.J. Acheson, T. Mullin

не подтвердили работоспособность маятниковой теоремы. Области

устойчивости, получаемые по маятниковой теореме, не согласуются с

экспериментальными результатами (см. рис. 2). Отметим, что заявлен-

ная авторами цель статьи заключалась именно в проверке работоспо-

собности маятниковой теоремы D.J. Acheson.

Проверим расчетные результаты статьи D.J. Acheson, T. Mullin.

Как уже указывалось, расчетные результаты (граничные линии обла-