О причинах расхождения результатов расчета и эксперимента при определении границ устойчивости обращенных стабилизируемых маятников (по материалам статьи D.J. Acheson, T. Mullin в журнале Nature)

О причинах расхождения результатов расчета и эксперимента…

Инженерный журнал: наука и инновации

# 2·2017 11

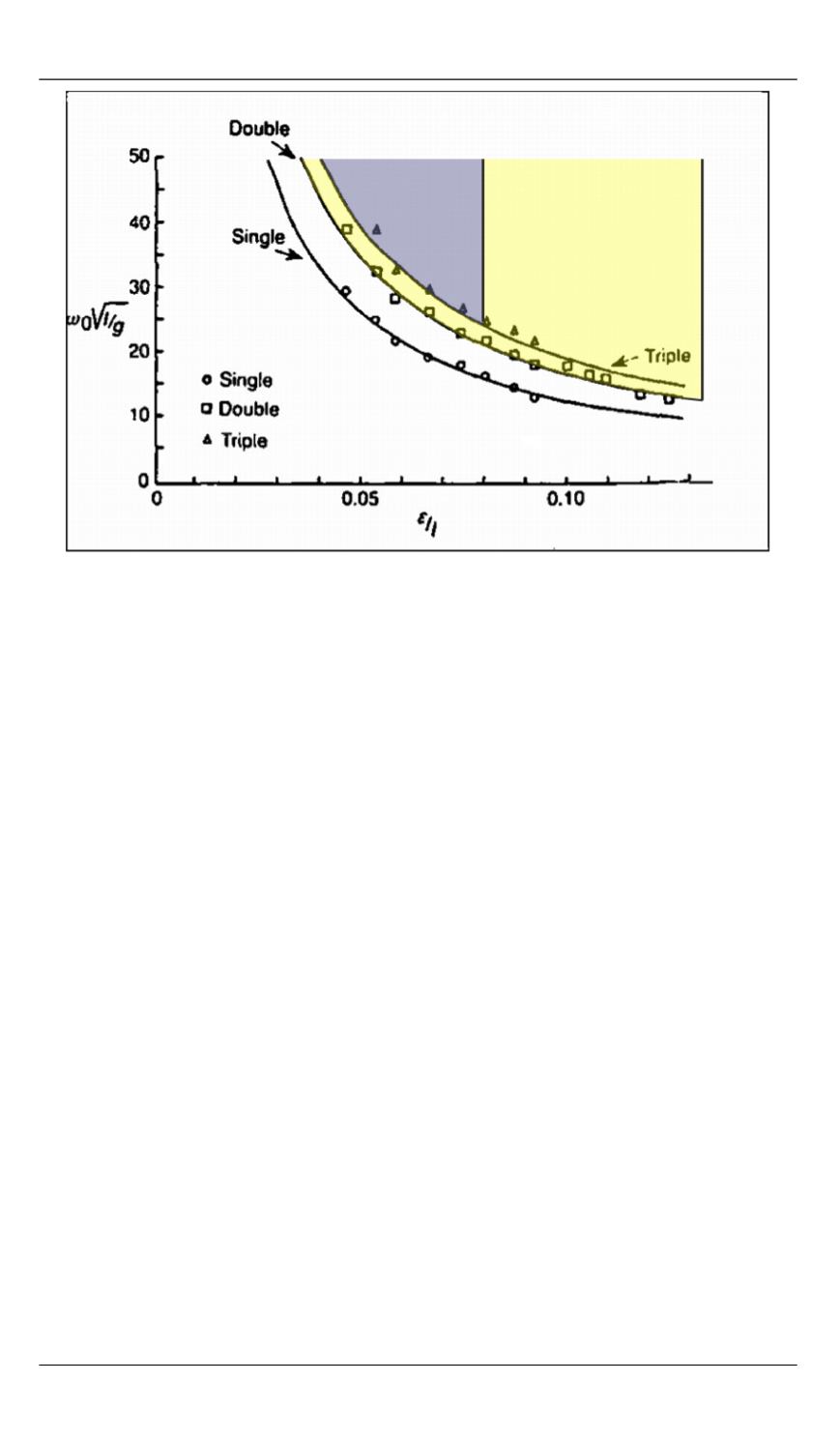
Рис. 8.

Уточненные области устойчивости маятников D.J. Acheson, T. Mullin:

— тройного;

— двойного

Режим динамической неустойчивости не наблюдался D.J. Acheson,

T. Mullin потому, что для двойного маятника перехода через динами-

ческую границу не было, а для тройного переход был слишком незна-

чительным, чтобы скомпенсировать погрешности расчета, вызванные

введенными допущениями.

По полученным уточненным результатам можно сделать вывод

о работоспособности маятниковой теоремы D.J. Acheson.

Дополнительная проверка маятниковой теоремы и проверка

достоверности полученных расчетных результатов.

Выполним

дополнительную проверку маятниковой теоремы D.J. Acheson. Для

этого используем расчетные и экспериментальные области устойчи-

вости обращенного тройного маятника с проверенными геометриче-

скими и физико-механическими параметрами [15]. Достоверность

параметров маятника доказана, поскольку при их определении с по-

мощью различных инструментов получены одинаковые значения.

В работе [15] границы области устойчивости определены с ис-

пользованием теории Флоке. Эти результаты представлены на диа-

грамме (рис. 9) сплошными линиями; экспериментально полученные

данные отмечены маркерами. Результаты, найденные с применением

проверяемой маятниковой теоремы, отображены пунктирной линией.

По вертикальной оси на рис. 9 отложена амплитуда параметриче-

ского возбуждения в миллиметрах, по горизонтальной — частота

возбуждения в герцах.