
В.А. Грибков, Я.Д. Гордин
10
Инженерный журнал: наука и инновации
# 2·2017
Результаты расчетов в SW масс отдельных элементов маятников
и маятников в целом, по которым получены приведенные в табл. 3
собственные частоты, представлены в табл. 1. В табл. 2 сведены
инерционные и геометрические параметры звеньев, необходимые для
расчетов.
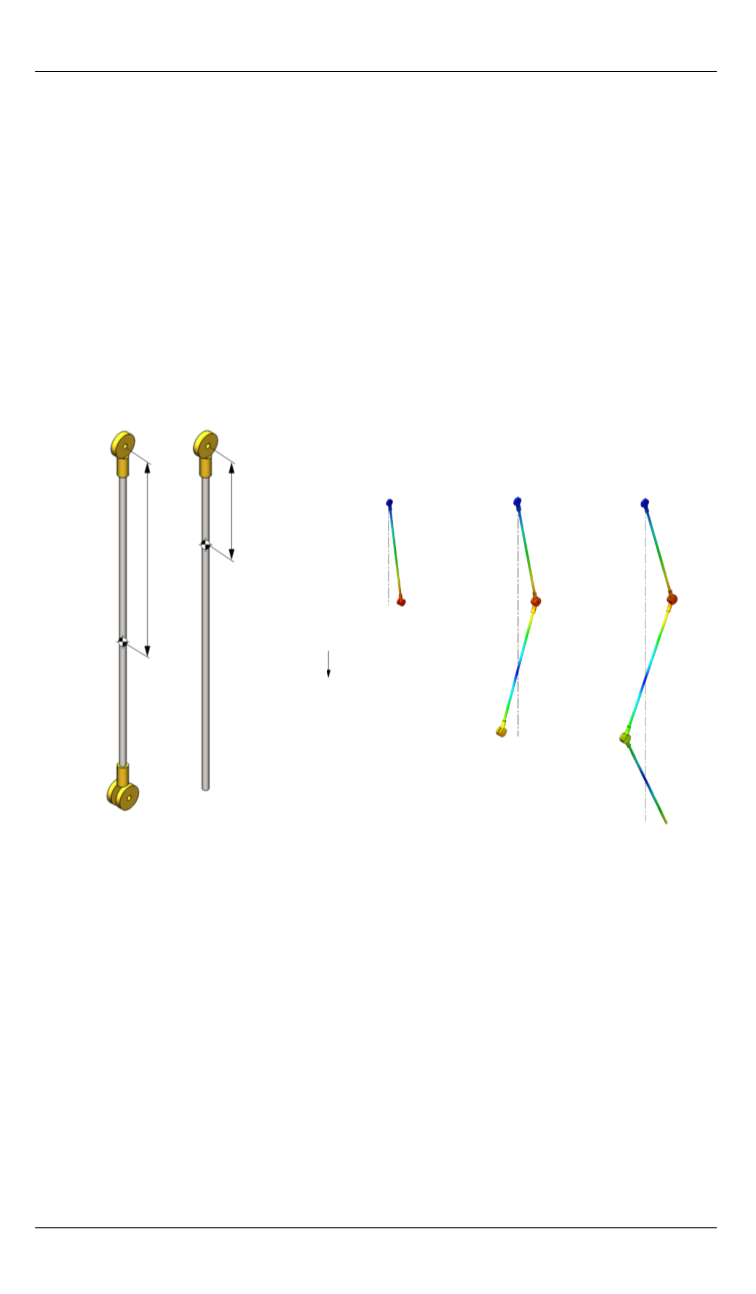
На рис. 6 изображены звенья тройного маятника, созданные в
SW, указаны положения центров масс и расстояния
сi
l
от оси корне-
вого шарнирного узла до центра масс звена.
На рис. 7 в качестве иллюстрации приведены собственные формы
колебаний одинарного, двойного и тройного маятников. Собствен-
ные формы колебаний двойного и тройного маятников показаны для
высших собственных маятниковых частот.
Рис. 6.
Положение центра масс
звеньев маятника, отсчитывае-
мое от оси корневого шарнира
(прямой маятник):
а
— корневое и среднее звенья;
б
— концевое звено
Рис. 7.
Собственные формы маятниковых
колебаний, соответствующие высшим соб-
ственным частотам (расчет в SW)
Представим области устойчивости, полученные по маятниковой
теореме [14] с использованием уточненных значений собственных
частот для двойного и тройного маятников, на диаграмме (рис. 8).
При сопоставлении результатов, полученных в эксперименте
и расчетом, видно, что области устойчивости после уточнения пара-
метров стали значительно больше (см. рис. 2, 8). Все эксперименталь-
ные точки для двойного и большинство значений для тройного обра-
щенных маятников попадают в уточненные области устойчивости.
107,253
53,741
а
б
g
















