
В.А. Грибков, Я.Д. Гордин
12
Инженерный журнал: наука и инновации
# 2·2017
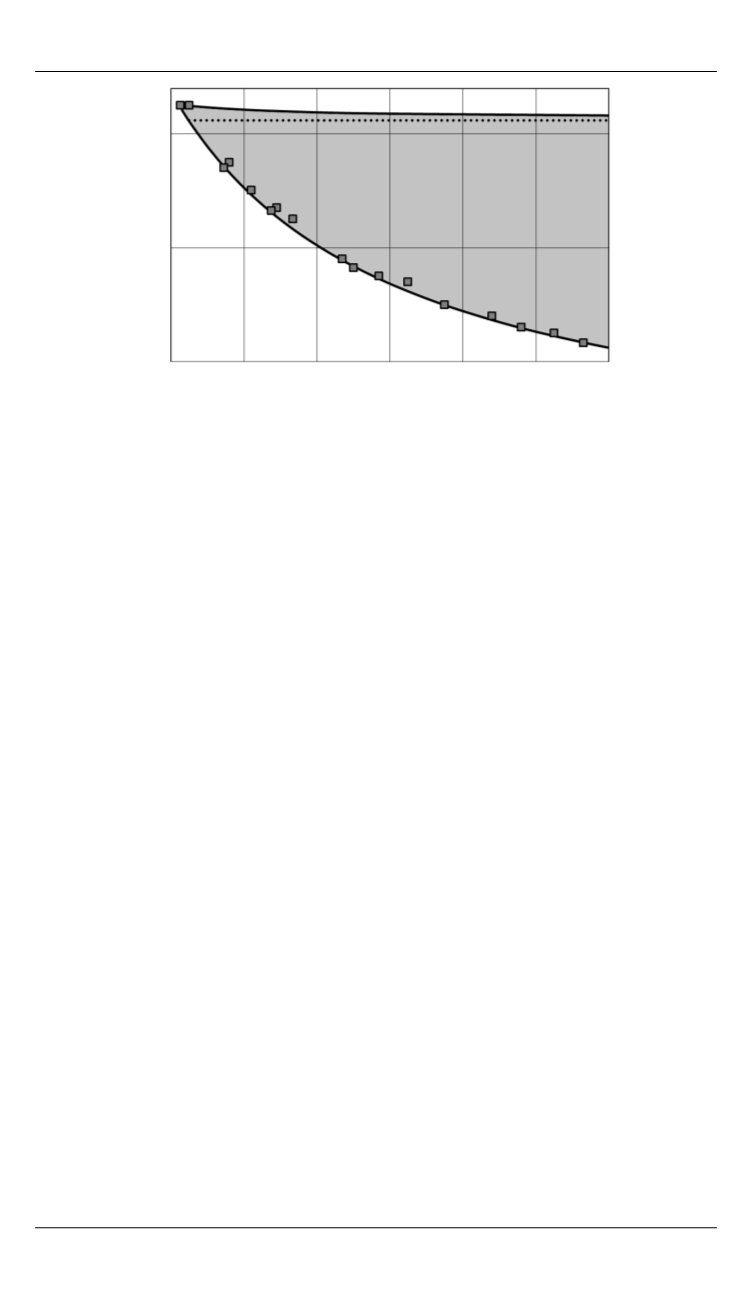
Рис. 9.
Диаграмма устойчивости тройного обращенного
маятника с параметрами из [15]
Нижняя криволинейная граница области устойчивости (квазиста-
тическая), полученная по маятниковой теореме, совпадает с резуль-
татами, полученными по теории Флоке. Верхняя прямолинейная гра-
ница области устойчивости (динамическая граница), определенная
с помощью формулы (1), имеет некоторые расхождения с верхней
криволинейной границей, определенной по теории Флоке.
Дополнительная проверка показала, что теорема D.J. Acheson рабо-
тает, но определяет верхнюю динамическую границу области устойчи-
вости с некоторыми отклонениями от истинных значений. Лучшие ре-
зультаты (с меньшей погрешностью) получаются для маятников со
значительно различающимися высшей и низшей собственными часто-
тами. Чем больше это различие, тем ближе верхняя граница к прямой
линии. Таким образом, область применения теоремы ограничена маят-
никовыми системами из нескольких звеньев с сильно различающимися
высшей и низшей собственными частотами.
Заключение.
Получены геометрические и инерционные пара-
метры, необходимые для динамических расчетов и решения задачи
устойчивости трех маятников из известной статьи D.J. Acheson и
T. Mullin в журнале Nature. Найдена причина радикального расхож-
дения расчетных и экспериментальных результатов для областей
устойчивости двойного и тройного маятников в статье D.J. Acheson и
T. Mullin: низкая точность экспериментального определения высших
собственных частот колебаний двойного и тройного прямых маятни-
ков, полученная через параметрические резонансы.
Границы области устойчивости двойного и тройного маятников,
рассчитанные по маятниковой теореме D.J. Acheson с использовани-
Амплитуда, мм
3
2
1
60
80
100
120
140
160
180
Частота, Гц
















