
С.З. Свердлов
12
Инженерный журнал: наука и инновации
# 11·2016
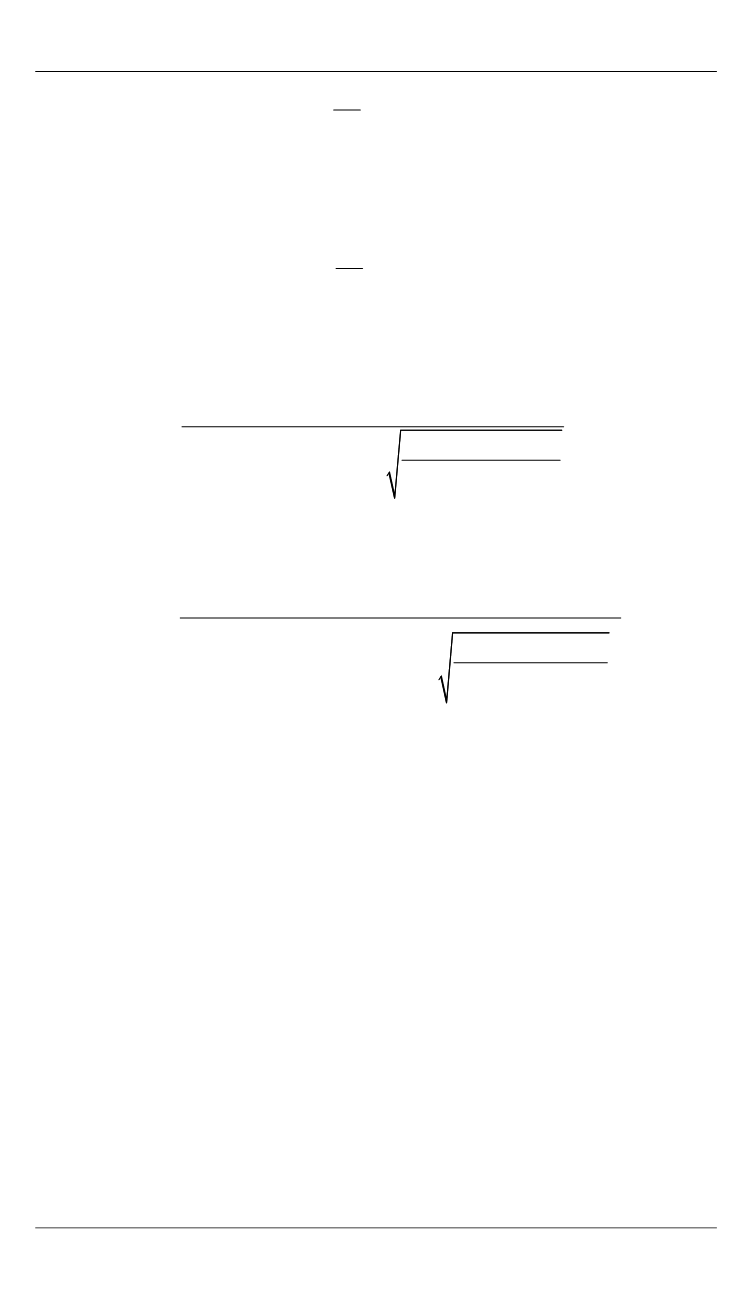
2 5
1 ( )
.
2
M
n D
= ρβ λ
π
(30)
Формулу (30) можно непосредственно использовать для вычис-
ления величины
M
из выражения (29). Для вычисления
M
100
необхо-
димо подставить β(λ) = β
0
и
n
=
n
100
в формулу (30):
2 5
100
0 100
1
.
2
M
n D
= ρβ
π
(31)
Подставив выражения для
M
,
n
,
M
100
,
n
100
в формулу (29) и вы-
полнив элементарные преобразования, получим зависимость КПД
мотора от коэффициента скорости λ:
(
)
100 0
0
100 0
100
2
.
1
( )
( )
M
T
y
k
R
η β
η =
α
η β ( − η β λ
α λ − λ
(32)
Перемножив КПД пропеллера и КПД мотора, получим КПД вин-
томоторной группы (ВМГ):
(
)
(
)
100 0
ВМГ
0
100 0
100
2
( )
.
( )
1
( )
( )
T
y
k
R
λα λ η β
η =
α
β λ η β ( − η β λ
α λ − λ
(33)
Значение λ, при котором достигается максимум функции (33),
можно определить численным методом, как численно найдены зна-
чения λ
опт
, приведенные в табл. 1, 2. Однако это значение, в отличие
от λ
опт
для пропеллера, зависит от тяговооруженности, жесткости ме-
ханической характеристики мотора и лобового сопротивления. Поэтому
делать такие расчеты заранее и табулировать их нерационально.
Вместе с тем оказывается, что вычисляемый по формуле (32)
КПД мотора незначительно изменяется в интересующем нас диапа-
зоне значений λ при обычном сочетании параметров мультикоптера.
Зависимости КПД пропеллера APC 12×45MR, КПД электромотора
(η
100
= 0,65) при трех вариантах параметров, а также КПД соответ-
ствующих ВМГ представлены на рис. 4.
Как видно, значение λ, соответствующее максимуму КПД винто-
моторной группы, незначительно отличается от λ
опт
пропеллера. Еще
меньше отличие от своего максимального значения в величине КПД
винтомоторной группы при λ = λ
опт
. Это позволяет использовать зна-
чения λ из табл. 1 и 2 для расчета оптимального и квазиоптимального
вертикального подъема. При этом погрешность таких расчетов, в ко-
















