
Применение методов имитационного моделирования…
Инженерный журнал: наука и инновации
# 7
2016
9
2
sin Ω ;
e
5
Ω.
Здесь
a
— большая полуось орбиты;
e
— эксцентриситет;
i
—
наклонение плоскости орбиты;
Ω
— долгота восходящего узла;
—
аргумент перигея;
— истинная аномалия.
Обратный переход от неособенных переменных к кеплеровым
элементам орбиты или прямоугольным координатам осуществляется
по формулам, приведенным в таблице.
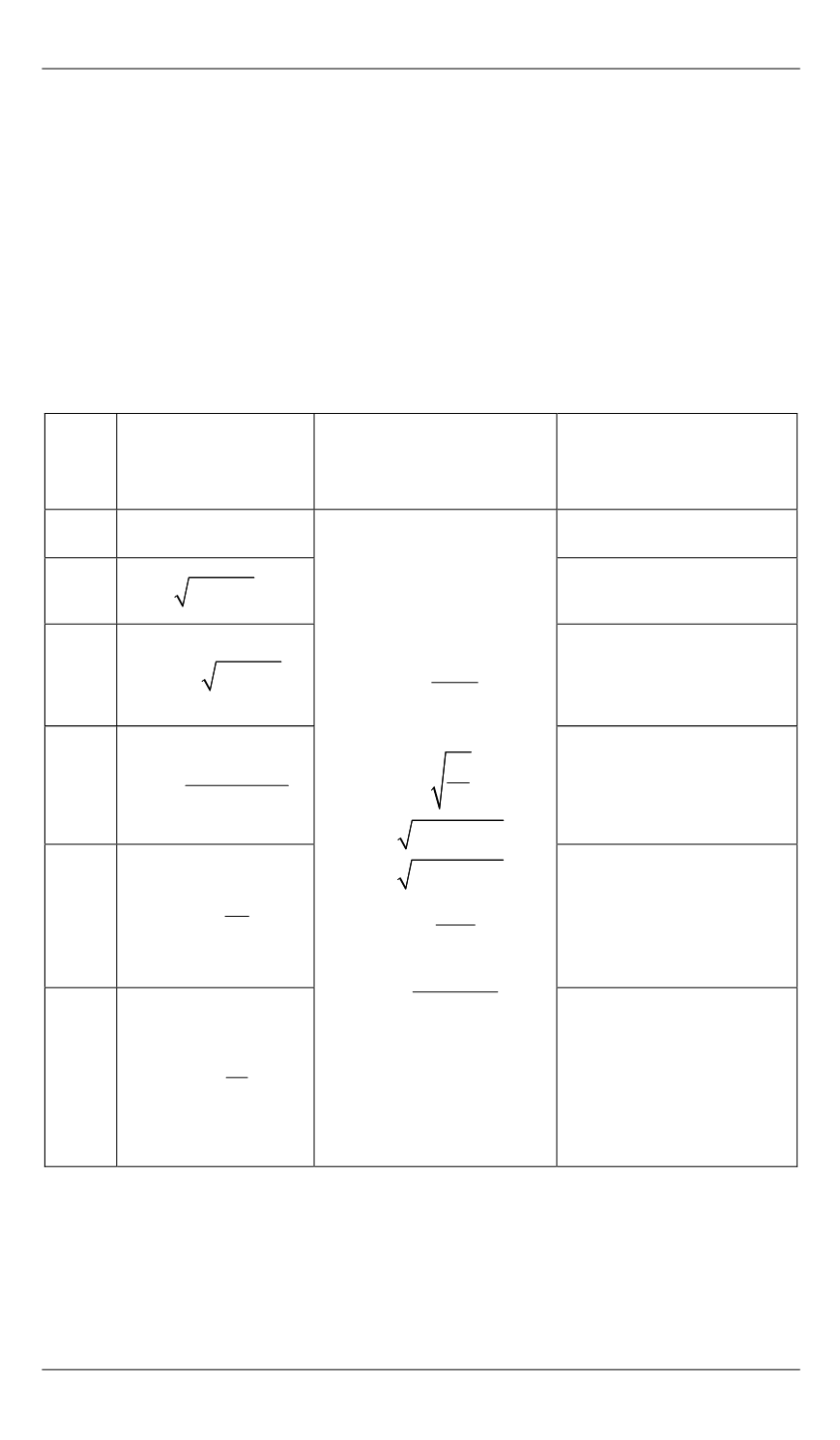
Формулы перехода от неособенных λ-переменных к кеплеровым элементам
и прямоугольным координатам
Кепле-
ровы
эле-
менты
Формула перевода
Дополнительные
параметры
Прямоугольные
координаты
и скорости
a
0
1
1
5
2
5
cos
sin
P
2
1
5
2
5
sin
cos
P
3
3
5
4
5
cos
sin
P
4
3
5
4
5
sin
cos
P
5
1
1
P
P
6
0
P n
3
n
a
2
2
1
2
1
2
2
3
4
1
c
2 6
r
P P
V
6
1
1
u
P P
V
5
r P a
1
5
4 4
cos
cos
2
P
2
5
3 4
cos
sin 2
P
3
4
cos
2
cP
1
cos
x r
e
2
2
1
2
2
cos
y r
i
2
2
3
4
2arctg
3
cos
z r
2 3
1 4
1 3
2 4
arctg
1
1
cos
cos
x
r
u
V V
V
Ω
4
3
arctg
2
2
cos
cos
y
r
u
V V
V
2
1
arctg
P
P
3
3
cos
cos
z
r
u
V V
V
Система дифференциальных уравнений, описывающих движение
КА в неособенных переменных, преобразованная к независимой пе-
ременной
5
, имеет следующий вид [8]:
















