
Д.А. Маслов
8
Инженерный журнал: наука и инновации
# 5 2016
Принимаем в системе уравнений (14) первый порядок точности
по
,
вводим безразмерные переменные
0
/4,
0
2
и умень-
шаем масштаб времени в 2 раза. Если действительные части всех
собственных значений матрицы системы
отрицательны, то
решения
системы уравнений (13) и, как следствие, системы (12) будут асимп-
тотически устойчивы.
Составим характеристическое уравнение
4
3
2
1
2
3
4
0,
a a a a
(15)
где
1
4;
a
2
2
2
0
2
0
2
6 2
;
a
0
3
2
2
2
0
2 2
2
;
2
)
(
a
4
2 2
2
2 2
0
0
0
4
4
0
0
1)
2 (
2 1
1 .
(
)
a
Согласно критерию
устойчивости Льенара —Шипара, для того чтобы многочлен (15)
имел все корни с отрицательными действительными частями, необ-
ходимо и достаточно, чтобы все коэффициенты полинома были по-
ложительными и, кроме того, выполнялось неравенство для минора:
2
1 2 3 1 4 0 3
(
)
0.
a a a a a a a
Учитывая, что коэффициенты
0
1,
a
1
4
a
положительны и условие
2
0
a
выполняется при
3
0,
a
представим
условия асимптотической устойчивости в виде системы трех нера-
венств:
2
2 2
0
0
2
2 2 4
2 2 2 2 4
0 0
0 0 0 0
2
2
2
2 2 4
2 2
0
0
0 0
0
2
0;
2
2
0;
1 2 2
2
16
0
16 16 8 4
16
.
(16)
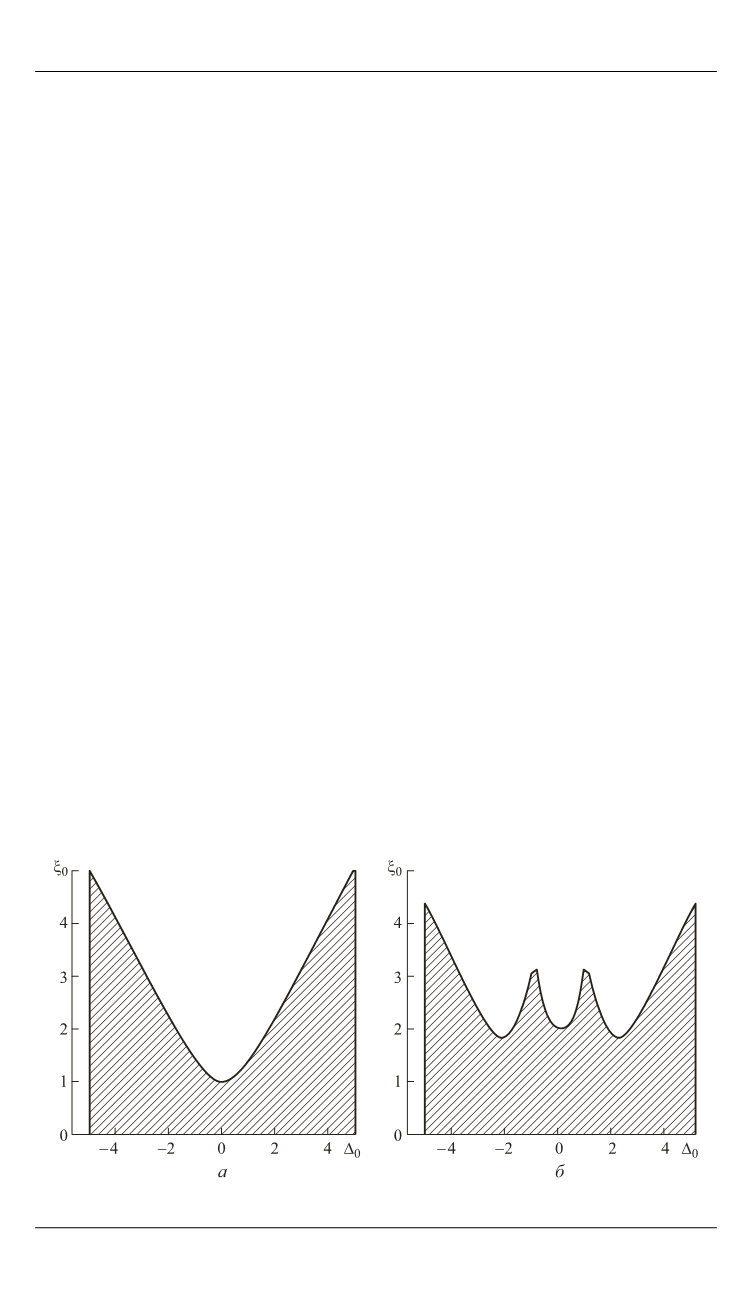
На рис. 2 области асимптотической устойчивости колебаний за-
штрихованы, по оси абсцисс отложена частотная настройка
0
,
по
Рис. 2.
Области асимптотической устойчивости колебаний
















