
И.Ю. Владимиров, Н.Н. Корчагин, А.С. Савин
2
Начало координат поместим на невозмущенной границе между
слоями жидкости, ось
x
направим вдоль этой границы, а ось
y
— вер-
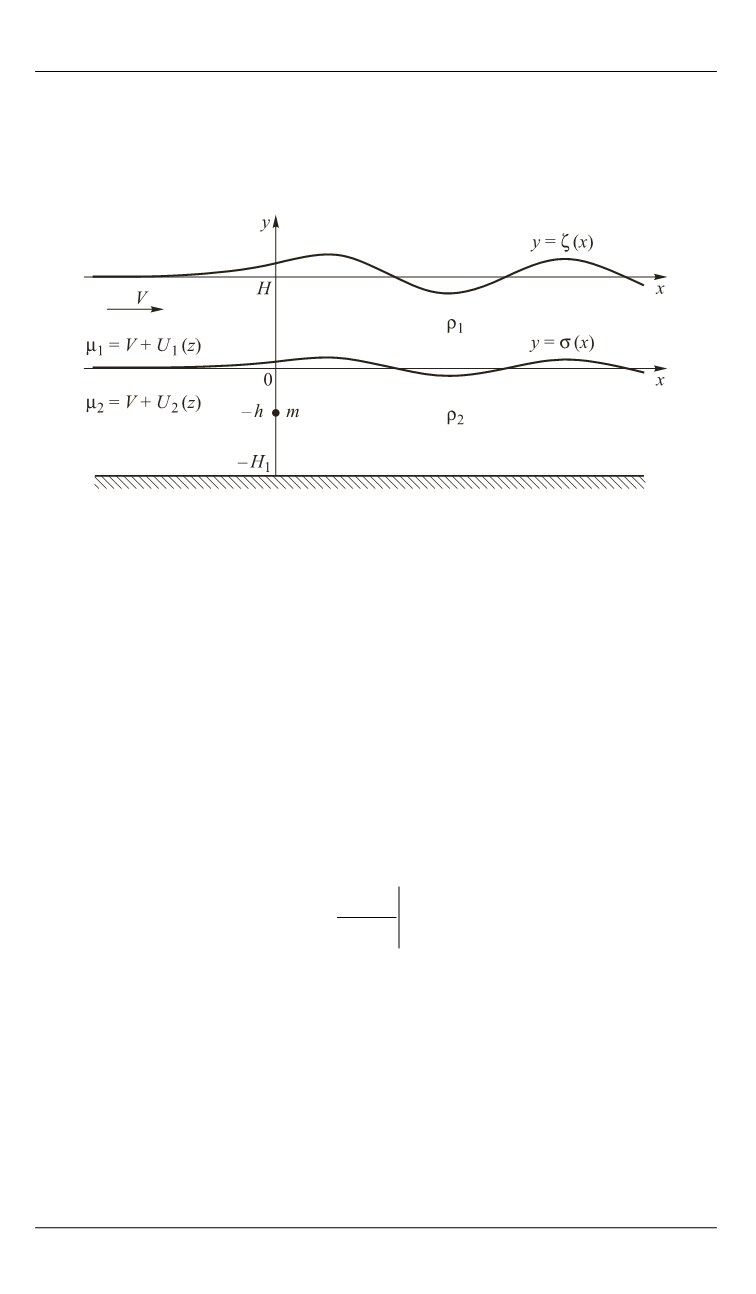
тикально вверх (рис. 1). Решение задачи проводим в рамках теории
малых возмущений.
Рис. 1.
Обтекание моделирующего трубопровод диполя, локализованного
в нижнем слое двухслойного потока
1. Вначале рассмотрим случай, когда
диполь находится под скач-
ком плотности
, т. е. в точке (0, –
h
). Пусть скорость установившегося
потока при
x
→ –∞ равна
V
. Предполагая течение потенциальным,
представим комплексно-сопряженную скорость в каждом из слоев в
виде
,
k
k
V U
k
k
k
v
U u i
,
{1 2}.
k
Обозначим отклонение
свободной поверхности от ее невозмущенного положения
y H
че-
рез
( ),
x
а возвышение границы раздела слоев потока — через
( ).
x
Вдоль линии тока
( )
y H x
вектор скорости произвольной ча-
стицы жидкости коллинеарен ее касательной. Отсюда
1
1
( )
.
( )
y H x
v x
V u
Далее, линеаризуя данное условие и перенося его со свободной
поверхности на прямую
,
y H
имеем кинематическое граничное
условие
1
при
( )
.
v
V x
y H
(2)
Аналогично получаем кинематическое условие вдоль поверхно-
сти раздела слоев
1
2
( )
( ) при 0
v V x v V x
y
(3)
Отсюда имеем одно условие для вертикальных компонент скорости:

















