
И.Ю. Владимиров, Н.Н. Корчагин, А.С. Савин
10
Что касается значений толщины верхнего и нижнего слоев, то был
рассмотрен случай, когда общая глубина потока
0
1
50 м,
H H H
а
толщина верхнего слоя
40 м.
H
С целью исследования влияния скач-
ка плотности на параметры обтекаемого потока локализацию центра
поперечного сечения трубопровода (т. е. моделирующего трубопровод
диполя) в модельных расчетах ограничили четырьмя горизонтами:
{1, 5; 2; 3; 4, 5}, м.
i
h
Результаты вычисления волнового сопротивления
X
и подъемной
силы
Y
(в расчете на 1 м погонной длины трубопровода) в зависимости
от скорости набегающего потока
V
приведены на рис. 2 и 3. На каждом
графике представлены четыре кривые, соответствующие разным рас-
стояниям
h
i
от диполя до слоя скачка плотности. На всех рисунках
уменьшение максимума сопротивления (см. рис. 2) и подъемной силы
(см. рис. 3) соответствует увеличению расстояния
i
h
от поверхности
раздела слоев до трубопровода, причем изменения значения максимума
волнового сопротивления и подъемной силы практически прямо про-
порциональны перепаду плотности ,
а скорость потока, при которой
достигается этот максимум, увеличивается при удалении трубопро-
вода от слоя скачка. В то же время модельные расчеты показали, что
значения величин
X
и
Y
практически не зависят от толщины слоев
потока
H
i
.
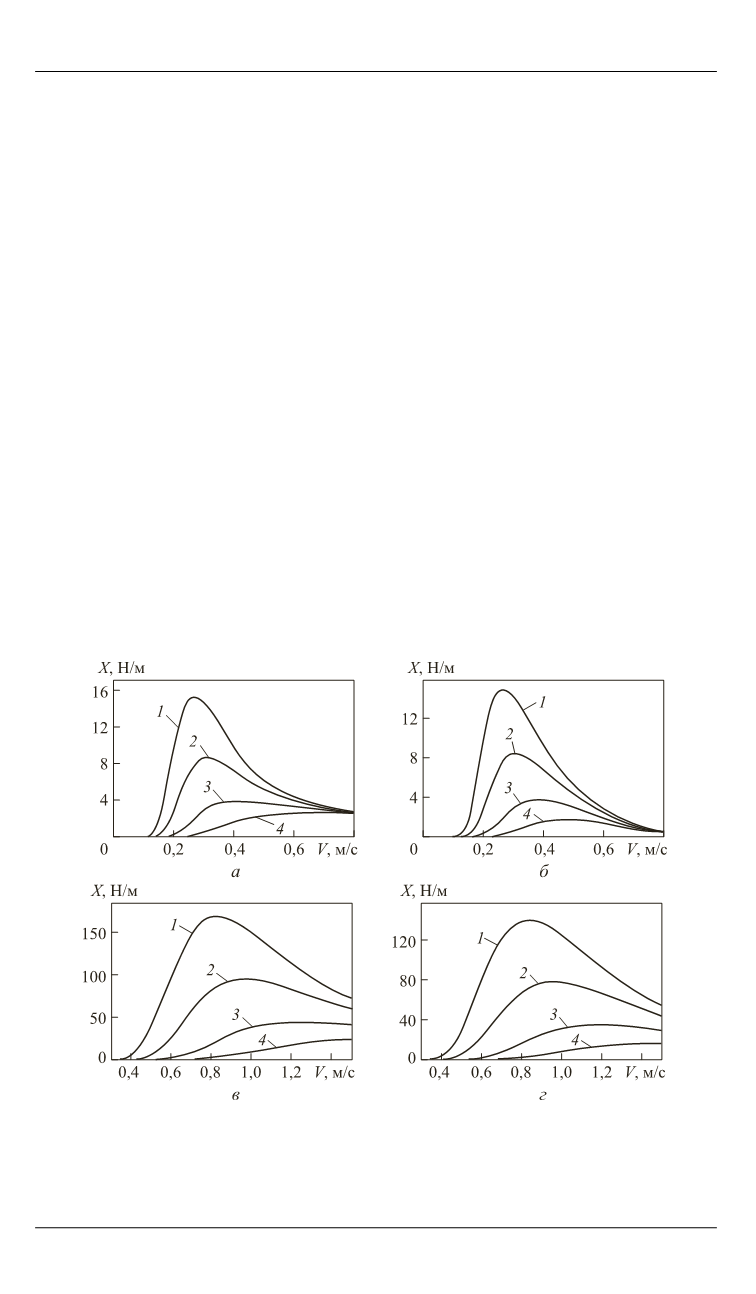
Рис. 2.
Зависимости волнового сопротивления от скорости потока при
2 1
/
1, 01
(
а
,
б
) и
2 1
/
1,10
(
в
,
г
); трубопровод находится под скач-
ком плотности (
а
,
в
) и над скачком (
б
,
г
):
1
—
h
= 1,5 м;
2
—
h
= 2 м;
3
—
h
= 3 м;
4
—
h
= 4,5 м

















