А.А. Гурченков, Л.А. Муравей, А.М. Романенков
6
ям (3), доставляющее минимум функционалу (11), с дифференциаль-
ными связями (9), (10) и начальными условиями (7).
Обозначим для краткости правые части уравнений (9) и (10) со-
ответственно через
Ф , ,
x
t
t
и
0
( , ),
.
x
F x t
t
Тогда вместо
(9) и (10) имеем
0
0
Ф , , ( ) 0;
, ,
.
x
x
t
t
t
dx F x t
t
dt
Докажем теперь возможность применения принципа максимума
Понтрягина для нашей задачи.
Будем называть управление ( )
a t
допустимым, если ( )
a t
— ку-
сочно-непрерывная функция, удовлетворяющая ограничениям (3).
Предположим, что ( )
a t
— некоторое допустимое управление, а
( , )
t x
и
0
( )
x t
соответствующие решения уравнений (9), (10) с усло-
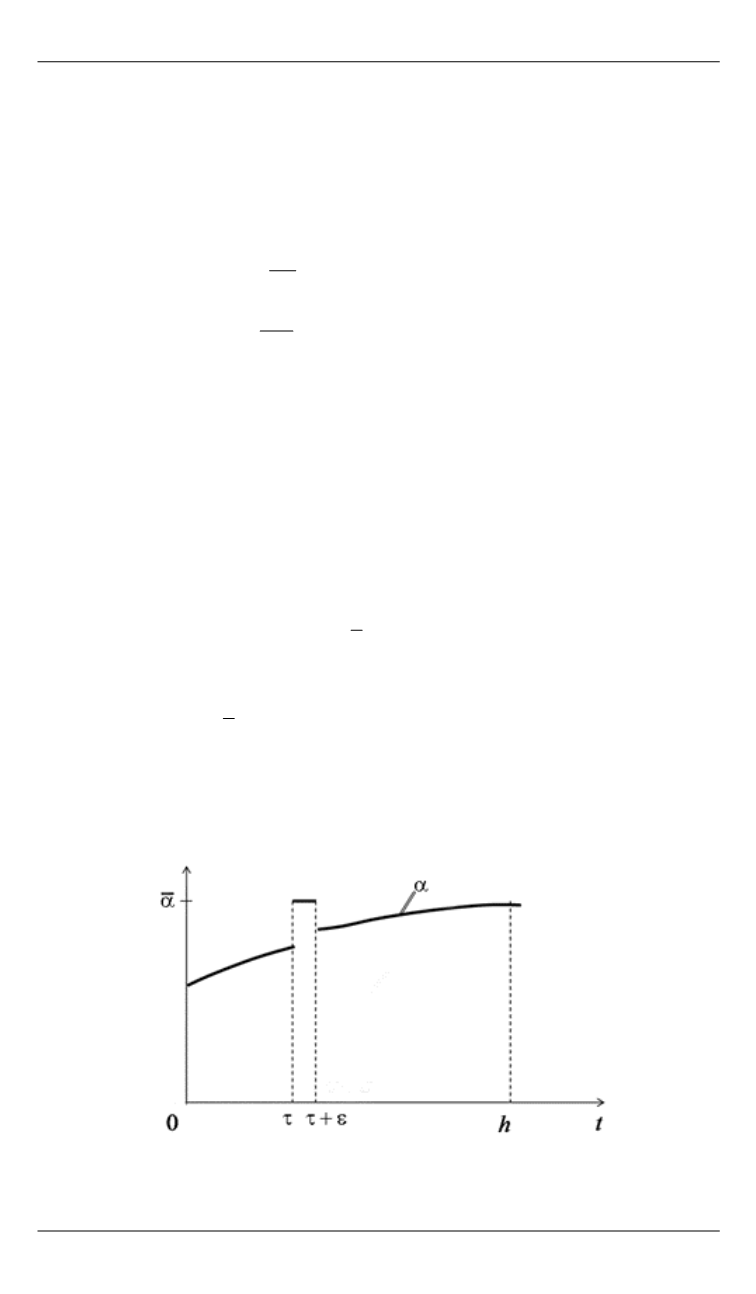
виями (7). Введем понятие сингулярной вариации управления
( ).
t
(рис. 3):
,
,
;
( )
( ),
,
.
a t
t
a t t
Здесь постоянная
a
такова, что
max
0 ( )
;
t
— заданная точка
непрерывности функции
( );
t
— произвольное положительное
число такое, что
0
.
T
Разность
( ) ( )
( )
t a t
t
будем
называть сингулярной вариацией управления.
Рис. 3.
Сингулярная вариация управления


