Моделирование и оптимизация технологического процесса ионно-лучевого травления
3
arctg
,
t
t
x
(2)
где
t
— угол между направлением падения ионного луча и осью
.
y
Будем считать
t
управлением, на которое наложены есте-
ственные ограничения:
max
0
.
t
(3)
В случае вращения в трехмерном пространстве уравнение ИЛТ
имеет вид (1), а формула для угла
будет следующей:
2
cos
, sin sin
cos
,
1
,
x
x
t
x t
t
t
t
x t
(2
)
где
— угловая скорость вращения маски [6–8].
Отметим, что рабочий слой при этом также распыляется, ско-
рость распыления зависит от угла между направлением ионного луча
и нормалью к поверхности и имеет вид, аналогичный функции
.
v
Обозначим эту функцию через
1
v
и будем считать, что процесс
травления прекращается, когда рабочий слой протравлен на глубину
h
. Нас будет интересовать скорость продвижения пограничной
(между защитной маской и рабочим слоем) точки
0
x
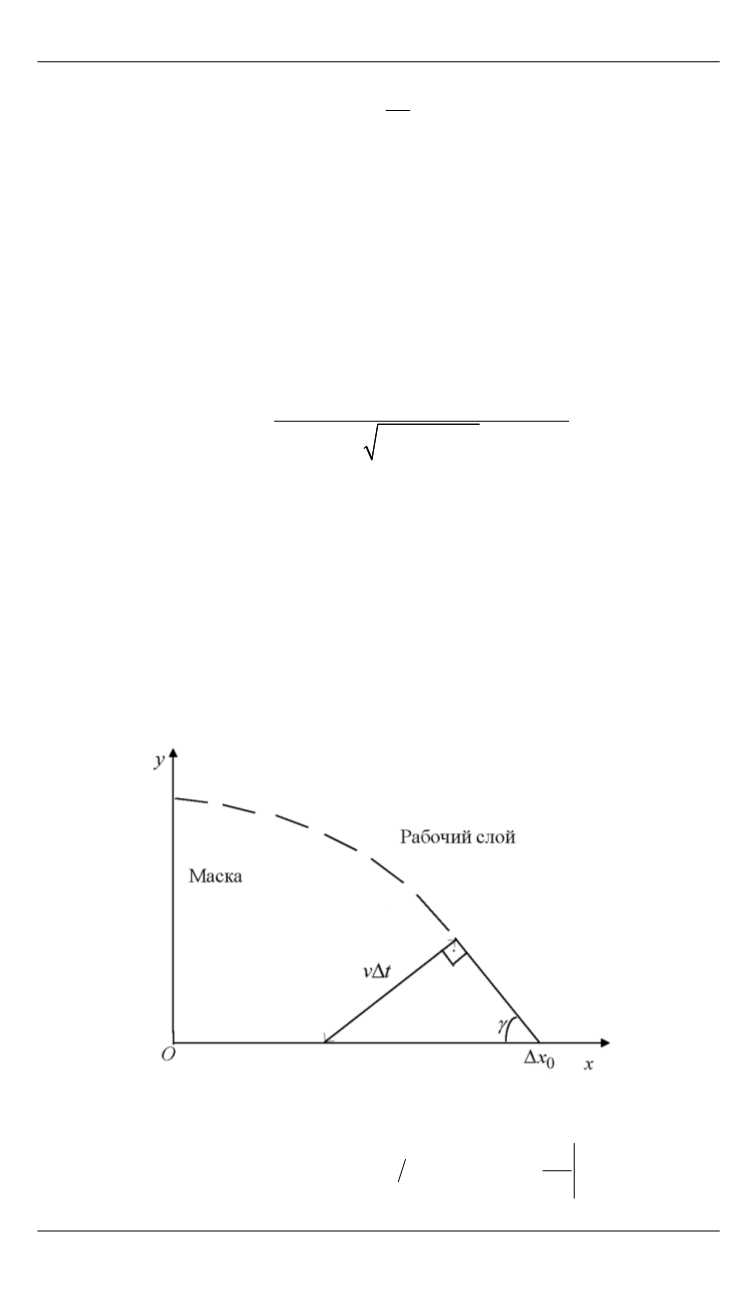
влево (рис. 2).
Рис. 2.
Схема продвижения точки
0
x
влево в результате ИЛТ
Несложно заметить, что
0
sin ,
x v t
0
arctg
,
d
dx
откуда


