Моделирование и оптимизация технологического процесса ионно-лучевого травления
5
Момент
T
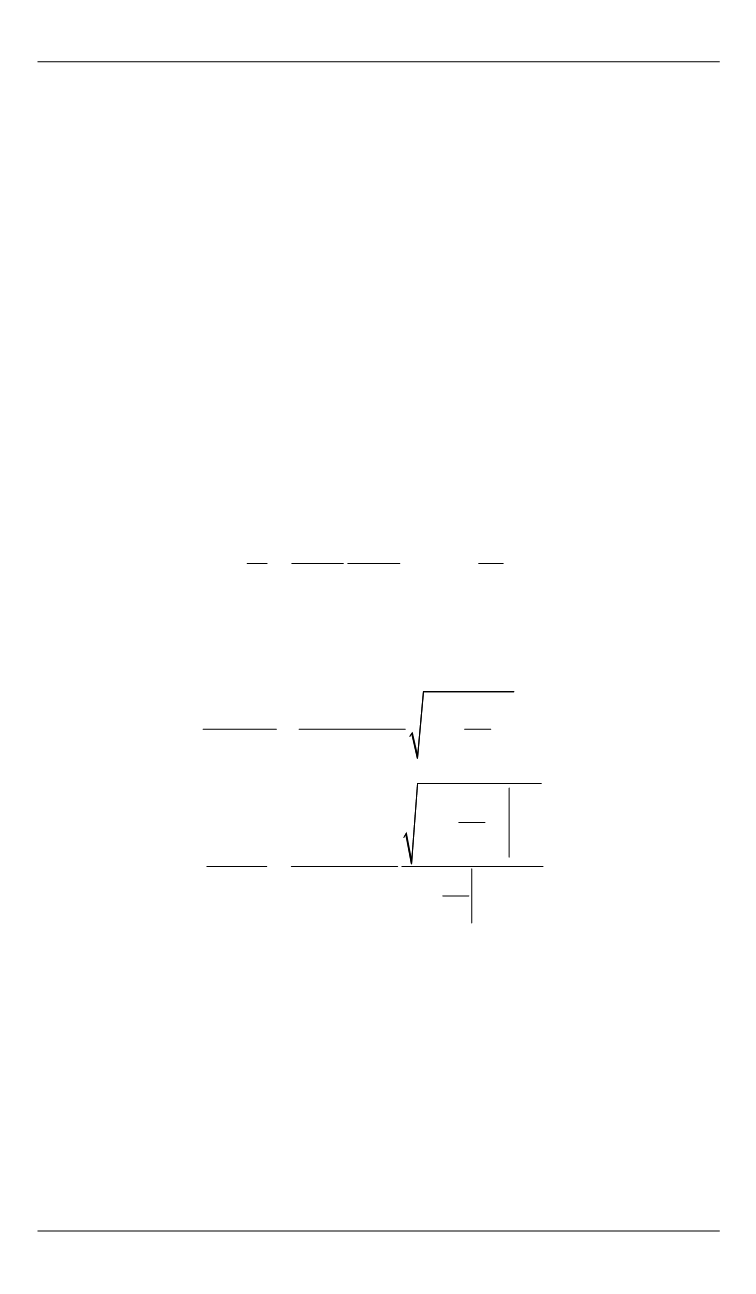
окончания процесса определяется из условия
1
0
.
T
v t dt h
(8)
Таким образом, имеем задачу с нефиксированным временем
T .
Это создает дополнительные трудности, так как помимо функций
t
и
,
t x
приходится искать и момент окончания процесса .
T
Но в данном случае легко перейти от задачи с нефиксированным
временем к задаче с фиксированным временем. Из формулы (8) не-
сложно заметить, что переменная
1
0
t
h t
v
d
является моно-
тонной функцией. Этот факт позволяет применить вместо перемен-
ной
t
новую переменную
,
h t
где
0
,
h t
h
т. е. получить задачу
с фиксированным временем. Осуществим этот переход. Согласно
формулам замены переменных имеем
1
.
dh t
v
t
h t
dt
h
Тогда уравнения (4), (5) примут следующий вид (снова переобо-
значим
h t
через
t
):
2
1
,
1
0;
v t
t x
t
v
x
(9)
2
0
0
1
0
1
.
x
v t
dx t
dt
v
x
(10)
Условия (7) и ограничение (3) на управление остаются без измене-
ний. Отметим, что решив задачу в такой постановке, можно легко
восстановить зависимость функций
t
и
,
t x
от «истинного»
времени .
t
В качестве минимизируемого функционала выберем величину
0
.
J t
x t
(11)
Таким образом, можно окончательно сформулировать задачу:
необходимо найти управление
,
t
удовлетворяющее ограничени-


