Плоская задача об упругом ударе тела о препятствие
9
Учитывая неравенство (14), получаем
1 2 0
0
2
.
Замечание.
Здесь и далее
*
arctg [0, ]
x
при
( ,
)
x
, т. е.
*
arctg , если 0,
arctg
arctg , если 0.
x
x
x
x
x
При этом
*
arctg ( )
2
;
*
arctg 0
x
, если
0
x
и
0
x
;
*
arctg
x
, если
0
x
и
0
x
.
Отметим, что характер движения точки контакта
S
в процессе
удара зависит от направления скорости точки
S
до удара и не зависит
от ее модуля. Введем угол
*
arctg ,
n
u
u
где
0 , ,
который является углом падения точки
S
, отсчитывае-
мым от касательного к опорной поверхности направления (рис. 1).
Тип удара или характер движения точки контакта
S
в процессе
удара определяется соотношением значений угла трения
, угла па-
дения
и углов
,
( 0 ,1, 2 , 3)
i i
i
. Анализ условий (9–13), (15–16),
определяющих тип удара, показывает, что некоторые из этих условий
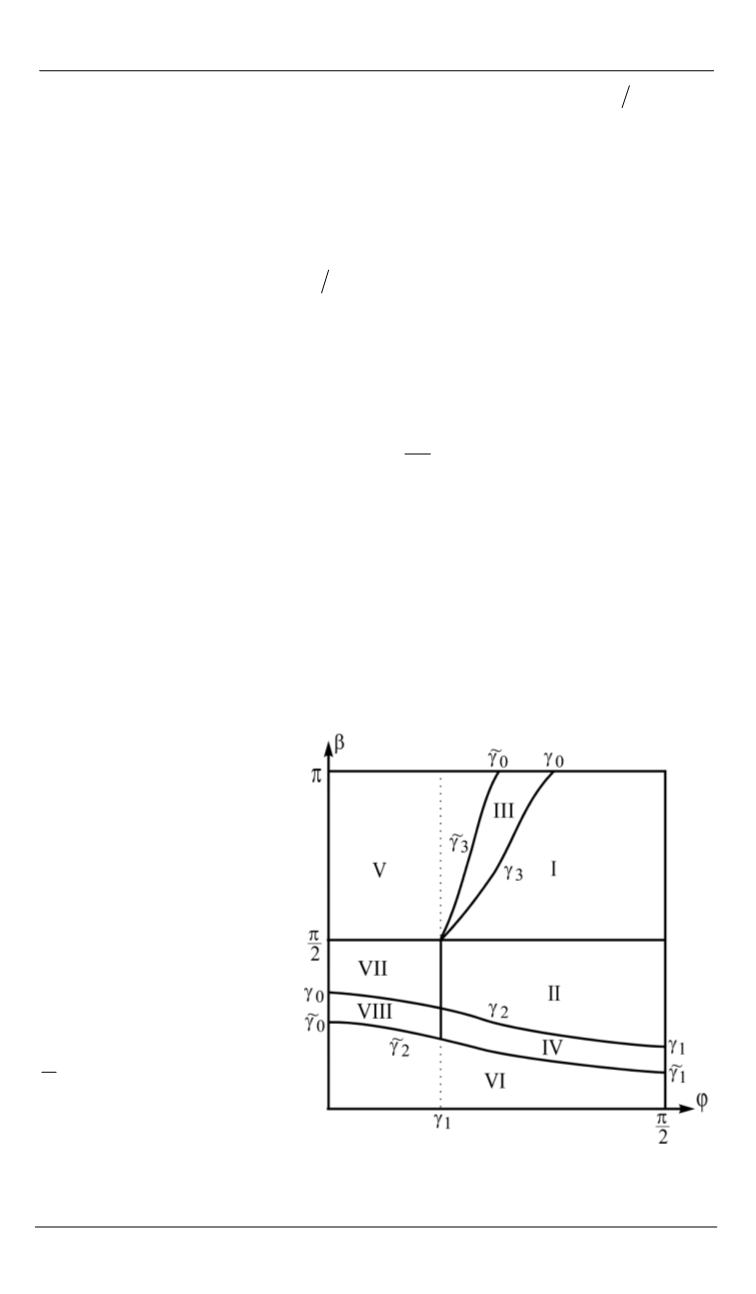
являются избыточными. На рис. 2 показаны области значений угла
трения
и угла падения
, которые соответствуют различным типам
ударов.
В качестве границ,
разделяющих эти обла-
сти, выступают кривые,
которые соответствуют
зависимости углов
2
,
3 2 3
, ,
от угла трения
.
Аналитически эти ус-
ловия имеют следующий
вид. В процессе удара
точка контакта
S
: в обла-
сти I, или при
1
,
3
,
2
скользит на-
право и останавливается
в фазе деформации; в об-
ласти II, или при
1
,
Рис. 2.
Области, соответствующие
различным типам удара


