В.В. Лапшин
2
Для случая
0
b
(центр
масс
C
лежит справа от точки
контакта
S
) все результаты мо-
гут быть получены из сообра-
жений симметрии.
Обозначим через
( , )
n
v v
v
касательную и нормальную
скорости центра масс
C
,
( , )
n
u u
u
— касательную и
нормальную скорости точки
контакта
S
,
— угловую ско-
рость тела. За положительное
примем направление угловой
скорости против хода часовой
стрелки. Скорости точек
C
и
S
связаны кинематическими со-
отношениями
,
.
n n
u v h u v b
(2)
Процесс удара разделим на две фазы: в фазе деформации нор-
мальная составляющая скорости точки контакта уменьшается до ну-
ля, оставаясь отрицательной, а в фазе восстановления — увеличива-
ется от нуля до некоторого положительного значения.
Нормальная скорость точки
S
до удара отрицательна, в конце фа-
зы деформации равна нулю, после удара положительна, а нормальная
составляющая импульса ударной силы реакции должна быть неотри-
цательной:
0,
0,
0,
0
n
n
n
n
u
u
u
R
. (3)
Значения всех скоростей до удара будем обозначать верхним индек-
сом «–» , значения скоростей после удара — «+», а значения скоростей в
конце фазы деформации (или начале фазы восстановления) — «'».
Уравнения удара (движения центра масс и изменения кинетиче-
ского момента тела относительно центра масс) в фазе деформации
имеют вид
2
(
)
,
(
)
,
(
)
,
n n
n
n
m v v R m v v R m
R b R h
(4)
а в фазе восстановления —
2
(
)
,
(
)
,
(
)
.
n n
n
n
m v v R m v v R m
R b R h
(5)
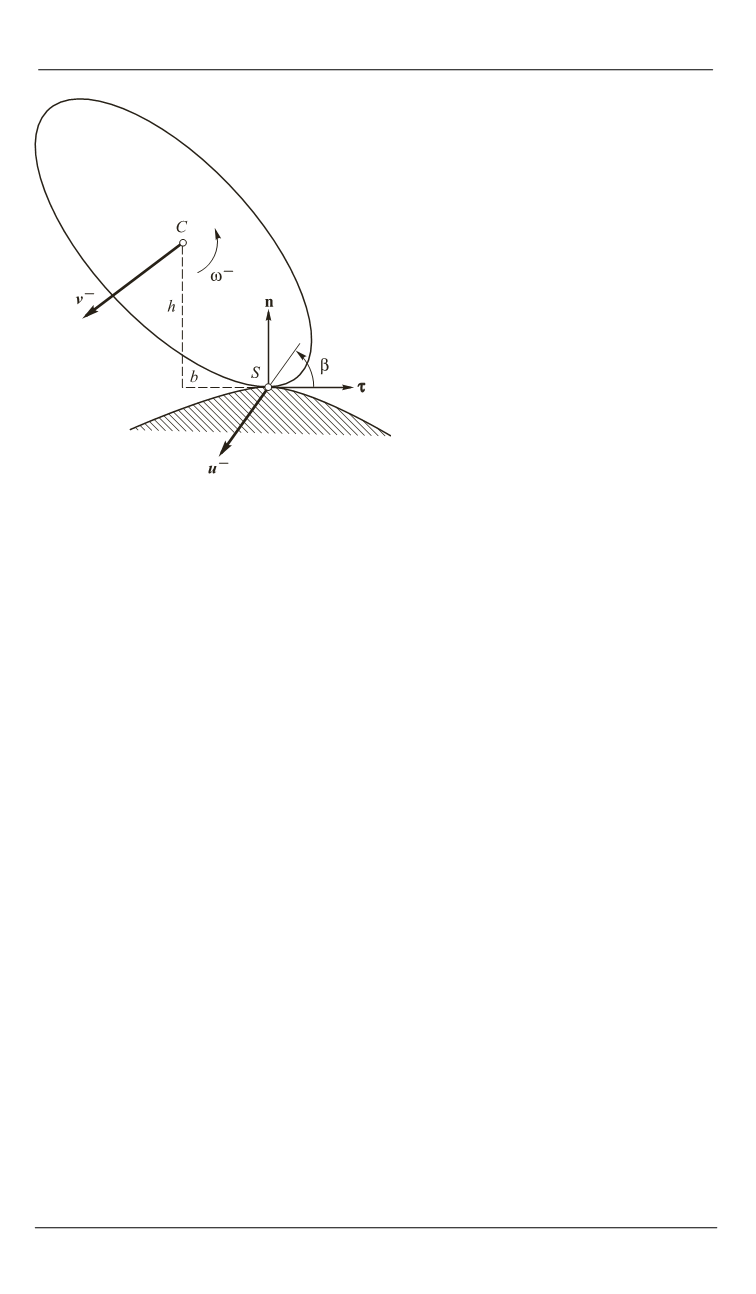
Рис. 1.
Схема взаимодействия
тела с препятствием


