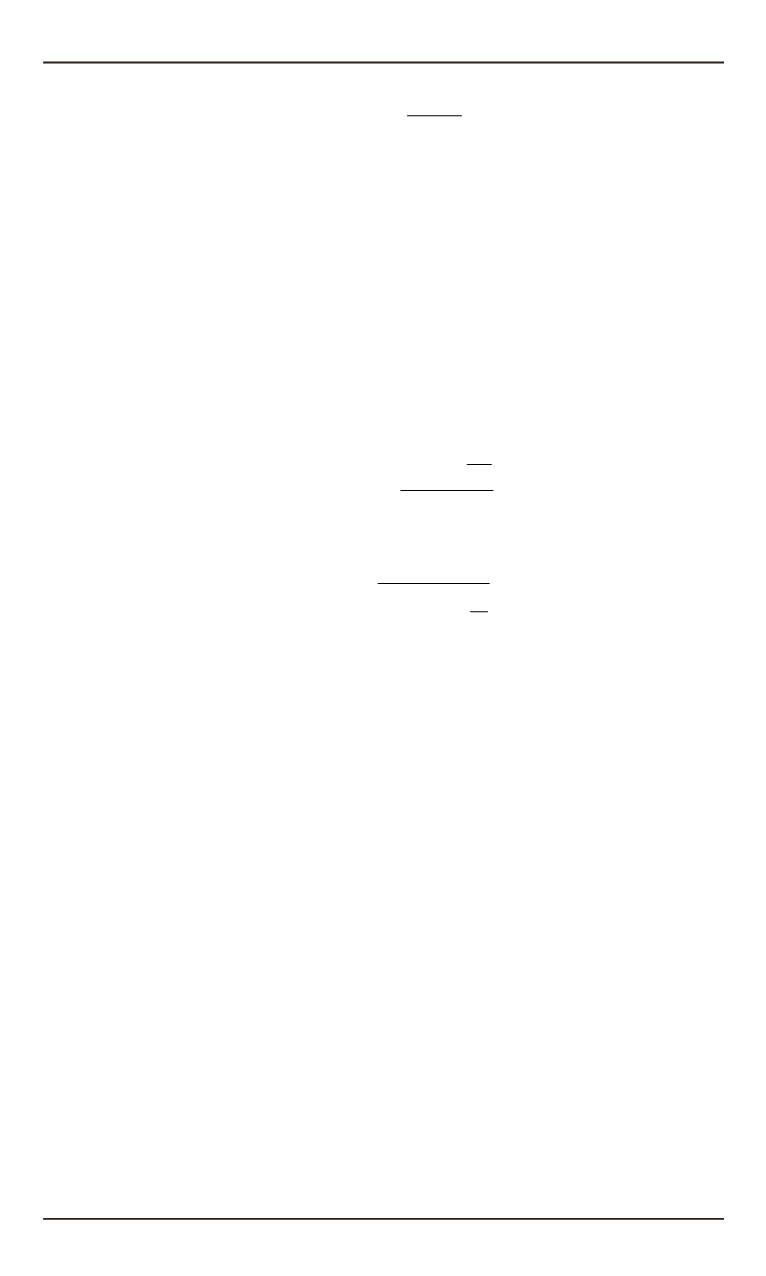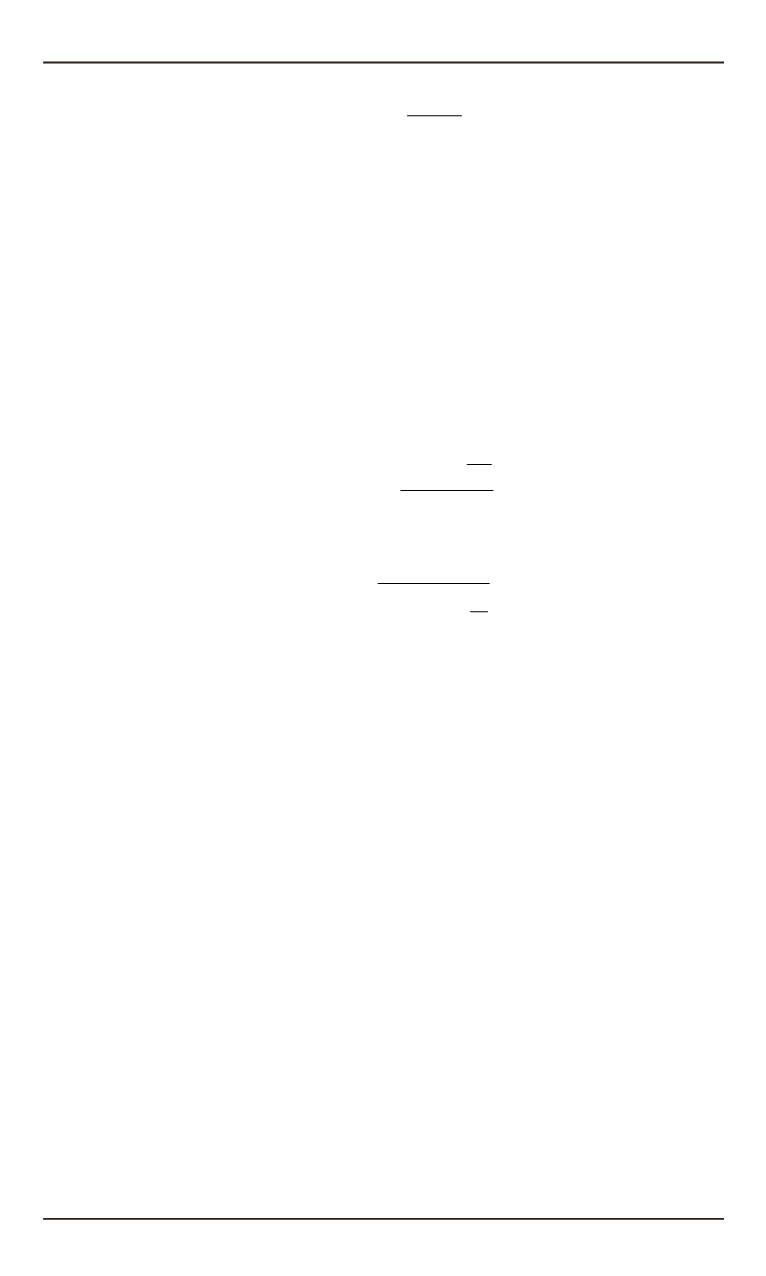
21
Кинетика зарождения локальных микродефектов при квазихрупком разрушении
p
p
0
( )
.
( )
k
k
t
t
t
p V
<
μ
Φ =
∑
Суммирование здесь идет по всем узлам, время распада которых мень-
ше
t
. При каждом значении аргумента
t
функция
Φ
p
(
t
) определяет от-
носительную долю узлов с временем распада, меньшим
t
. Количество
дырок в произвольный момент времени
t
равно числу узлов, время рас-
пада которых меньше
t
. Следовательно,
p
Φ
p
(
t
) в каждый момент равна
числу дырок в этот момент.
Функции распределения
F
р
(
ρ
)
≡
F
р
(
δ
n
), где
δ
n
=
Ωρδ
V
(
ρ
), и
Φ
p
(
t
)
связаны друг с другом, поскольку их аргументы связаны взаимно-об-
ратными функциями:
1
в
( ) exp
,
( )
.
ln
в
a b
n
t g n A
kT
b
n g t
t
a k T
A
+ +
+
−
+
σ
⎛
⎞
− ⎜
⎟δ
= δ = ⎜
⎟
⎜
⎟
⎝
⎠
δ = =σ
−
(20)
Эта связь функций распределения
F
р
(
ρ
) и
Φ
p
(
t
) выражается
формулами
F
р
(
ρ
) =
Φ
p
(
g
(
ρ
)),
Φ
p
(
t
) =
F
p
(
g
–1
(
t
)).
Функции распределения
F
р
(
ρ
)
≡
F
р
(
δ
n
) и
Φ
p
(
t
), как видно из их опре-
деления, представляют собой кусочно-постоянные разрывные функ-
ции и являются полными аналогами эмпирических функций распре-
деления математической статистики. С большой точностью их можно
аппроксимировать непрерывными и даже гладкими функциями
F
(
ρ
),
Φ
(
t
). Обе эти функции также назовем функциями распределения. Пер-
вая
F
(
ρ
) описывает распределение слабых узлов по их мощности. Вто-
рая
Φ
(
t
) описывает распределение дырок во времени и определяет от-
носительное количество дырок в момент времени
t
. Связь между этими
функциями распределения такая же, как и между их дискретными ана-
логами
F
р
(
ρ
) и
Φ
p
(
t
), т. е.
F
(
ρ
) =
Φ
(
g
(
ρ
)),
Φ
(
t
) =
F
(
g
–1
(
t
)).
(21)