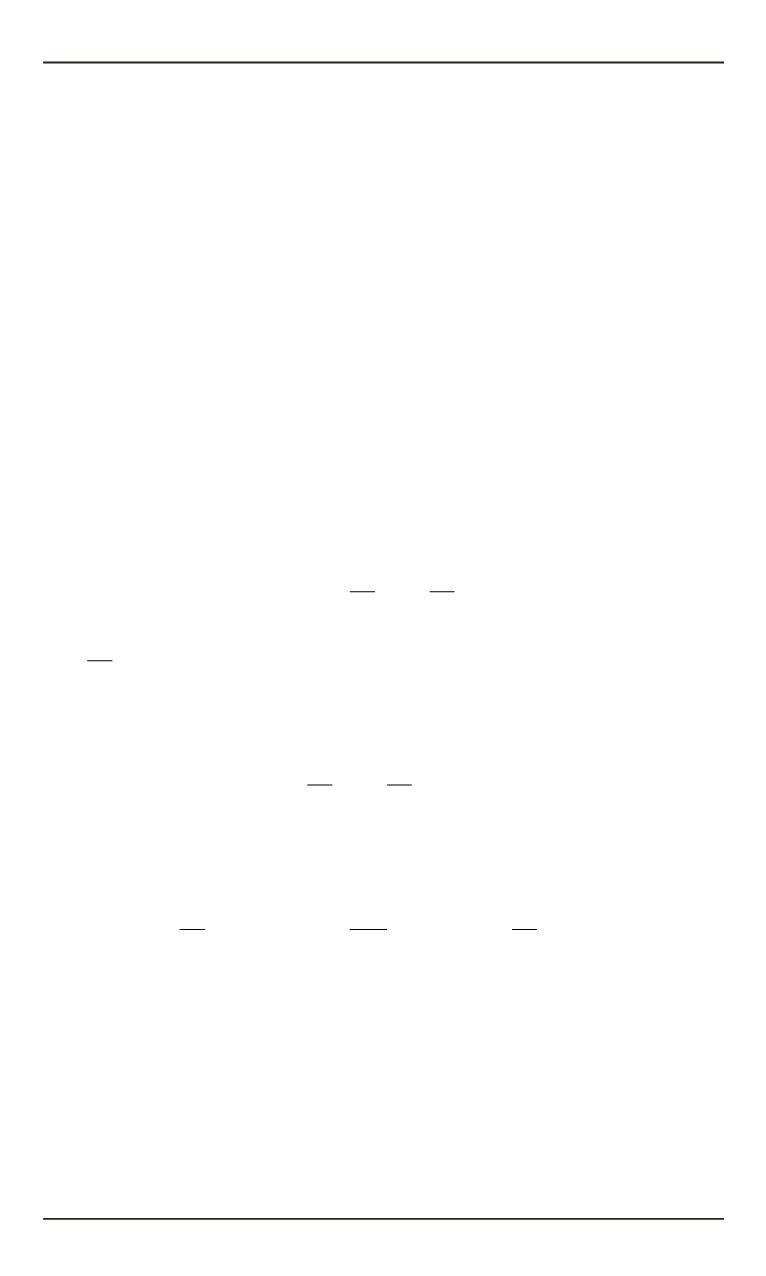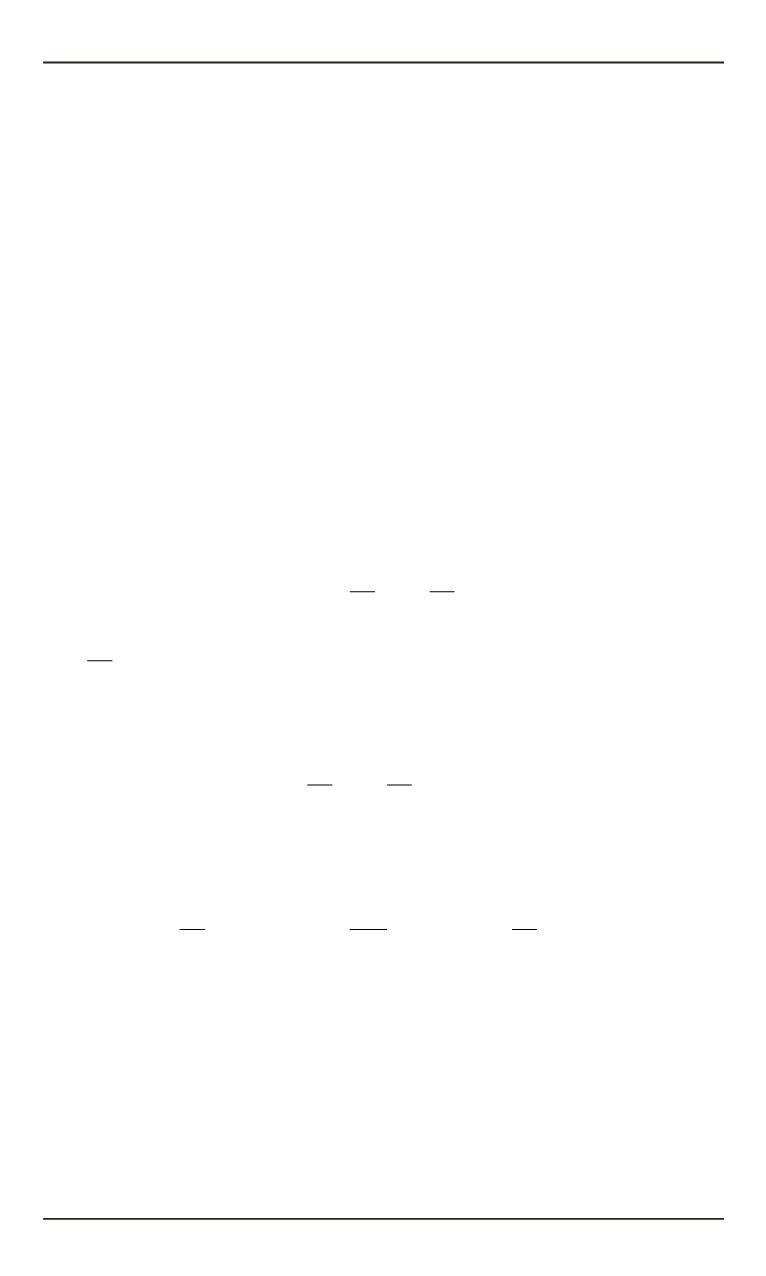
4
Ю.И. Димитриенко, А.А. Захаров, М.Н. Коряков, Е.К. Сыздыков, В.В. Минин
4
4
0,
=
,
,
s
g e
s
w w
q
= − λ∇θ ⋅
+ ε σθ − ε σθ θ = θ
v
n
(5)
где
q
e
= –
n
·λ
s
·
∇
θ — тепловой поток, который идет на нагрев конструк-
ции; θ
w
— температура твердой стенки; θ — температура газа на этой
стенке; θ
e
— температура внешней поверхности пограничного слоя;
ε
g
и ε
s
—интегральные коэффициенты излучения нагретого газа и твер-
дой поверхности; σ — коэффициент Стефана—Больцмана. Унос мате-
риала конструкции не учитывался.
На границе входа потока Σ
2
(сверхзвуковой и дозвуковой) задаются
следующие условия:
ρ = ρ
e
,
v
=
v
e
, θ = θ
e
,
(6)
где ρ
e
,
v
e
, θ
e
— заданные значения параметров; ρ
e
, θ
e
— параметры не-
возмущенного потока;
v
e
— вектор скорости набегающего потока.
На дозвуковой границе выхода потока Σ
3
задается одно условие,
и еще четыре формулируются при численной аппроксимации решения
[15]:
,
0,
0,
e
n
n
∂
∂θ
ρ = ρ =
=
∂
∂
v
(7)
где
n
∂
= ⋅∇⊗
∂
v n v
— нормальная производная вектора скорости. На
сверхзвуковой границе выхода потока Σ
4
граничные условия не зада-
ются, но при численной реализации формулируются условия
0,
0.
n
n
∂
∂θ
=
=
∂
∂
v
(8)
На плоскости симметрии Σ
5
(которая может и отсутствовать) зада-
ются следующие условия симметрии:
0,
0,
0,
1, 2,
0.
I
v
I
n
n
n
τ
∂
∂ρ
∂θ
= ⋅ =
= =
=
∂
∂
∂
v n
(9)
Начальные условия к системе (1)–(5) имеют вид
t
= 0: ρ = ρ
0
,
v
= 0,
E
=
c
V
θ
0
,
(10)
где ρ
0
, θ
0
— заданные значения.
Система уравнений внутреннего тепломассопереноса в кон-
струкции ГЛА.
Будем рассматривать элемент конструкции ГЛА,
обтекаемый внешним потоком, изготовленный из теплозащитного
композиционного материала на полимерной матрице с термостойки-