В.Ф. Апельцин, Т.Ю. Мозжорина
2
ственный метод теоретического исследования этих свойств подразу-
мевает численные методы математического моделирования, что и
делается в большинстве работ этого направления [4–5].
В данной работе приводится аналитический подход к решению
подобной задачи в случае одномерного фотонного кристалла с ко-
нечным числом слоев
N
. В рамках этого подхода удается выписать
явное решение для прошедшего через структуру и отраженного от
нее волновых полей, если потребовать выполнения некоторого не-
обременительного дополнительного условия, связывающего диэлек-
трические проницаемости слоев ячейки периодичности и их толщи-
ны. В результате, все практически важные физические свойства
структуры становятся наглядными и обозримыми.
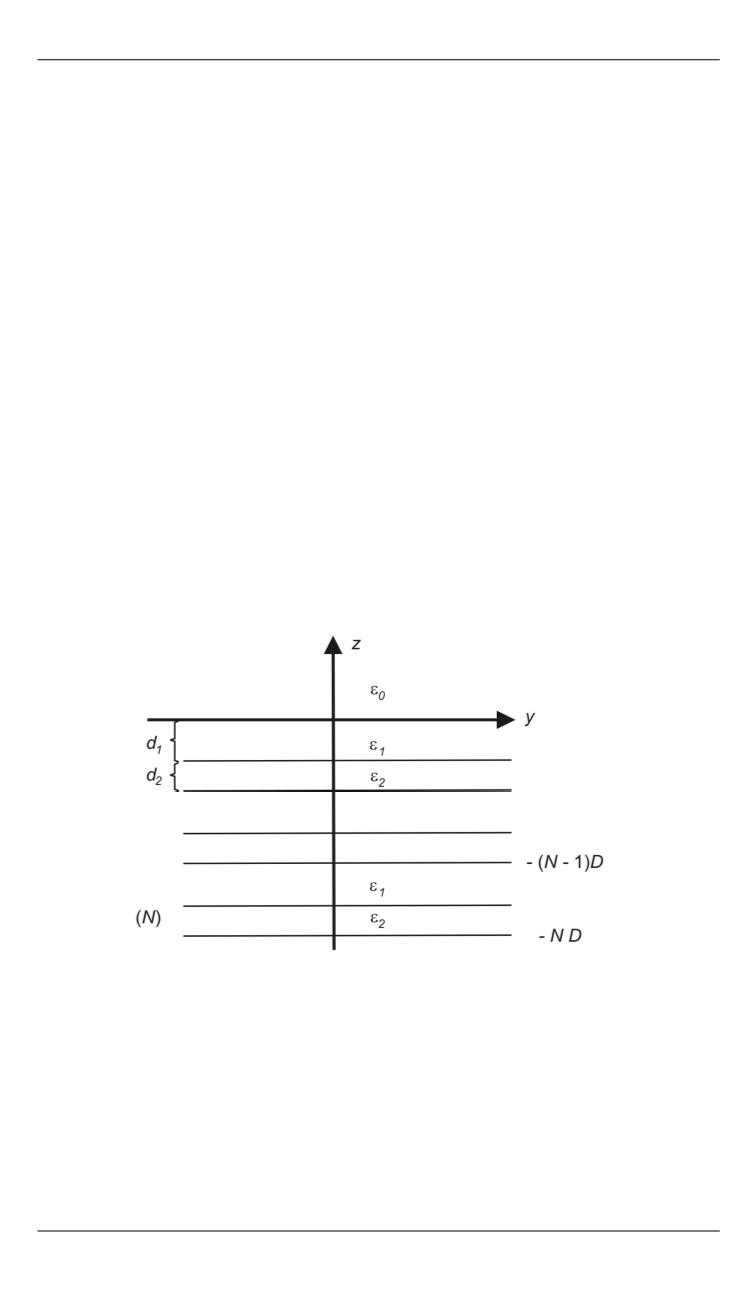
Постановка задачи и система уравнений для фурье-образов
решения.
Пусть в области декартовых координат (
y
,
z
) при
z
0 рас-
положена многослойная среда с плоскими параллельными границами
раздела, причем слои имеют периодичность по толщине и значению
диэлектрической проницаемости
. Элемент периодичности является
двухслойной плоской полосой с толщинами слоев
d
1
и
d
2
, общей
толщины
D = d
1
+ d
2
, и с диэлектрическими проницаемостями
1
и
2
.
Среда содержит
N
элементов периодичности. Общее количество сло-
ев 2
N
(рис. 1).
Рис. 1.
Геометрия одномерного фотонного кристалла
Структура возбуждается плоской волной
(0)
,
u y z
=
=
0
( cos
sin )
,
ik y
z
e
присутствующей в области
0
z
выше структу-
ры. Здесь же присутствует поле
0
,
u y z
, отраженное от структуры и
подлежащее нахождению. В области
z ND
присутствует про-
шедшее поле
2 1
,
N
u y z
,
также подлежащее определению.
Рассмат-
ривается случай
Е –
поляризации (единственная компонента
элек-


