Построение моделей кинематики исполнительных механизмов манипуляционных…
9
где
τ
13.Б
,
τ
11.Б
,
τ
12.Б
— матрицы поворота СК (
Х
13
,
Y
13
,
Z
13
), (
Х
11
,
Y
11
,
Z
11
),
(
Х
12
,
Y
12
,
Z
12
) относительно СК (
Х
Б
,
Y
Б
,
Z
Б
);
l
03.Б
,
l
01.Б
,
l
02.Б
— векторы,
связывающие начало СК (
Х
Б
,
Y
Б
,
Z
Б
) с началами СК (
Х
03
,
Y
03
,
Z
03
),
(
Х
01
,
Y
01
,
Z
01
), (
Х
02
,
Y
02
,
Z
02
);
l
13.03
,
l
11.01
,
l
12.02
—
векторы, связывающие начала СК, отмеченных
нижними индексами этих векторов.
В основе решения ОКЗ лежат соотношения
для расчета угловых координат каждого из двух
звеньев каждого из трех пальцев кисти. Будем
считать заданными линейные координаты нача-
ла СК, связанной с последними звеньями паль-
цев, относительно СК, связанных с основаниями
пальцев. Эти координаты являются компонен-
тами некоторого вектора
t
. Угловые координаты
звеньев обозначим
q
1
i
и
q
2
i
. Для решения по-
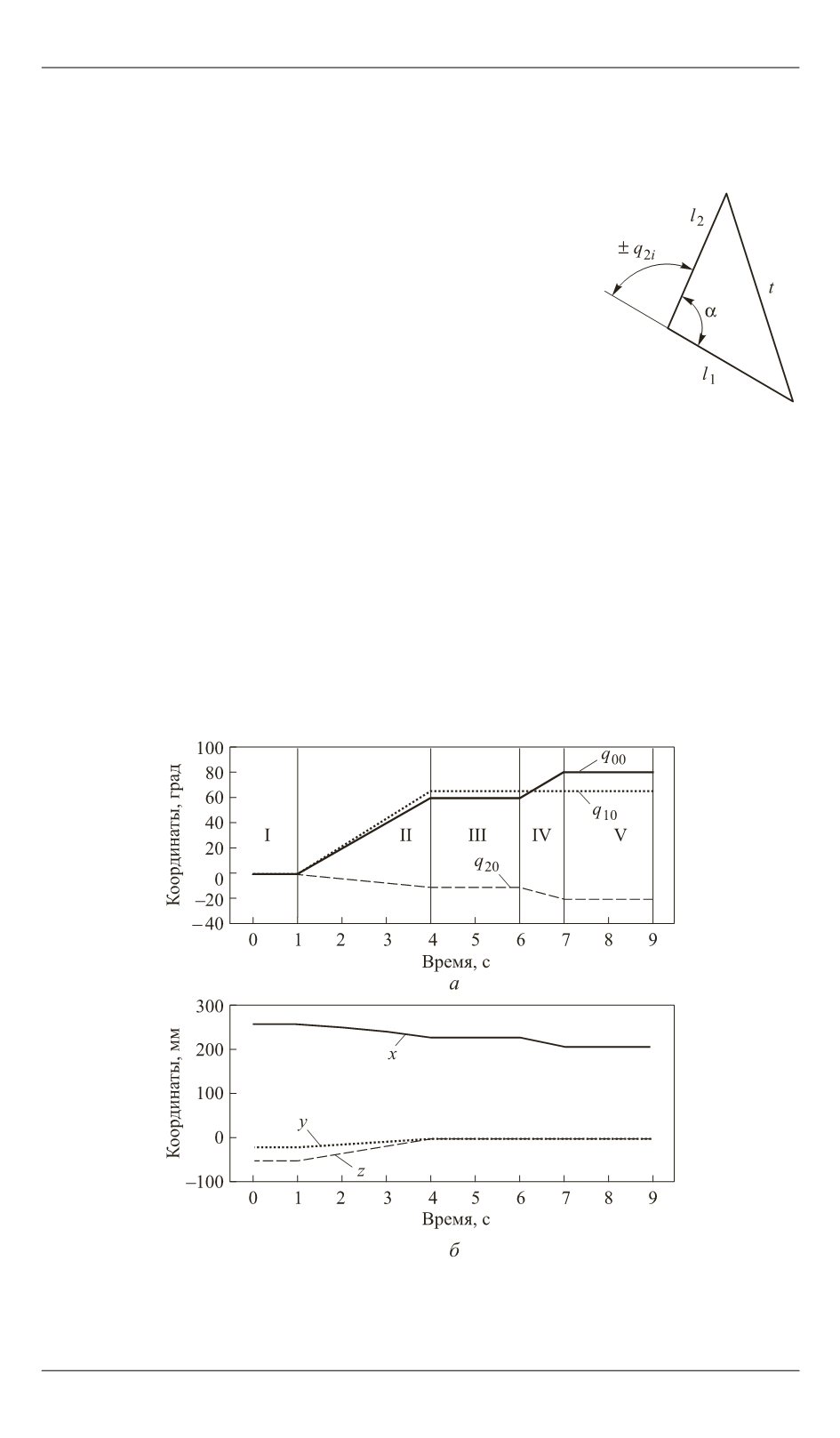
ставленной задачи рассмотрим треугольник на
рис. 3, где
t
— длина отрезка, связывающего начала СК основания и
последнего звена пальца;
l
1
,
l
2
— длины отрезков, связывающие нача-
ла СК двух звеньев одного пальца.
По теореме косинусов
2 2 2
1 2
1 2
cos (
)/(2 ),
l
l
t
l l
α = + −
тогда
q
2
i
=
= 180° ±
α
.
Рис. 3.
Расчетная
схема для опреде-
ления угловых ко-
ординат
Рис. 4.
Временные зависимости угловых координат поворота шарниров (
а
)
и декартовых координат конца третьего пальца (
б
):
I–V — временные интервалы


