М.Ф. Иванов
,
А.Д. Киверин
,
Е.Д. Шевелкина
12
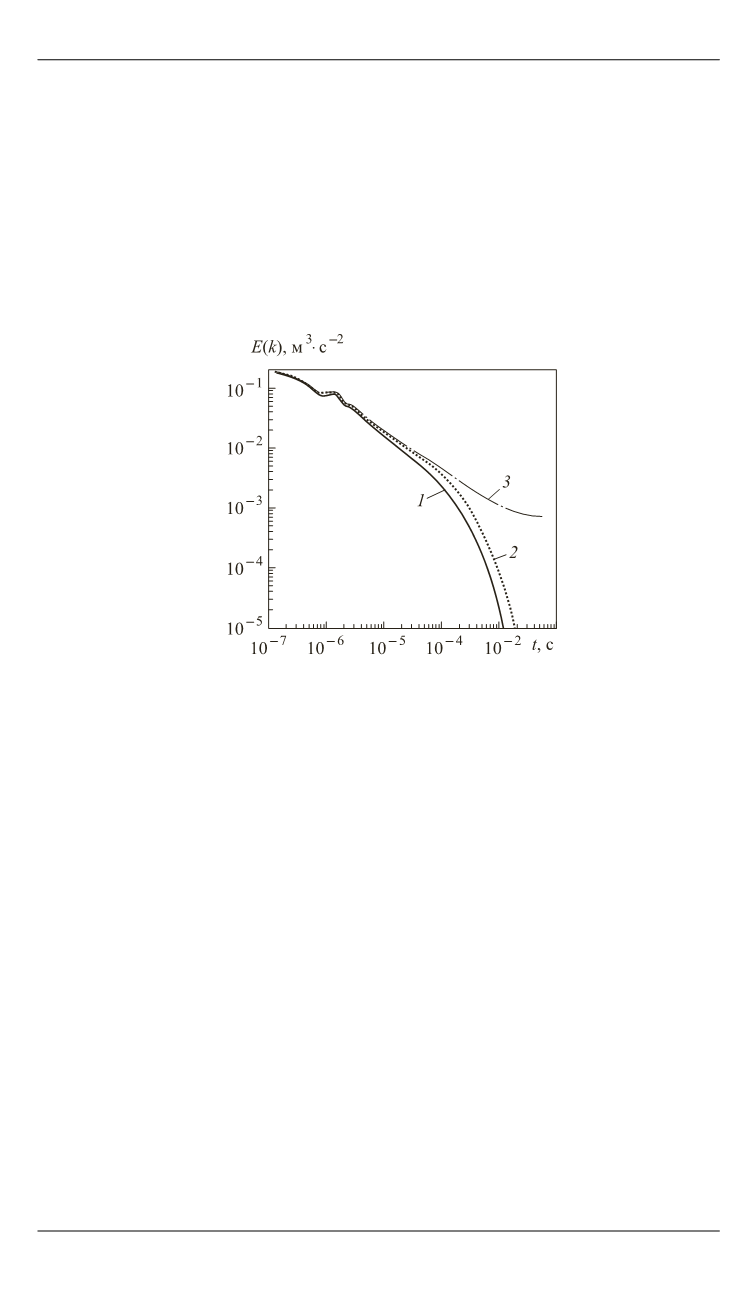
Это подтверждается зависимостями на рис. 5, где приведено из-
менение энергии возмущений во времени на стадии затухания турбу-
лентности для систем с разными граничными условиями. При этом в
задаче с проскальзыванием потока на границах диссипация энергии
возмущений обусловлена только описанным выше механизмом вяз-
кого рассеяния и поглощения энергии, а в случае торможения потока
на границах это условие является дополнительным фактором дисси-
пации энергии, что приводит к более быстрому затуханию турбу-
лентности.
Рис. 5.
Изменение энергии возмущений во времени на стадии затухания
турбулентности:
1
–
3
– течение с торможением потоков на стенках области с проскальзыванием по-
тока у стенок и с периодическими граничными условиями соответственно
Заключение.
Анализ результатов математического моделирова-
ния среды, формируемой задаваемыми стохастическими возмущени-
ями, которые развиваются по законам гидродинамики вязкого газа,
показал, что такая модель адекватно воспроизводит основные выво-
ды теории Колмогорова, подтверждаемой, в свою очередь результата-
ми лабораторных экспериментов и натурных наблюдений. Это, с од-
ной стороны, позволяет применять предложенный подход при компь-
ютерном моделировании ряда реальных турбулентных процессов (их
набор требует дополнительного анализа), а с другой – показывает,
что основные соотношения теории Колмогорова следуют непосред-
ственно из закономерностей эволюции хаотических возмущений в
газодинамической среде без дополнительных требований однородно-
сти и изотропии этой среды. Последнее подтверждается и прямым
компьютерным моделированием взаимодействия разномасштабных
вихрей в конвективных потоках, основанном на прямом численном
решении уравнений Навье – Стокса.


