А.В. Плюснин
,
И.А. Доденко
6
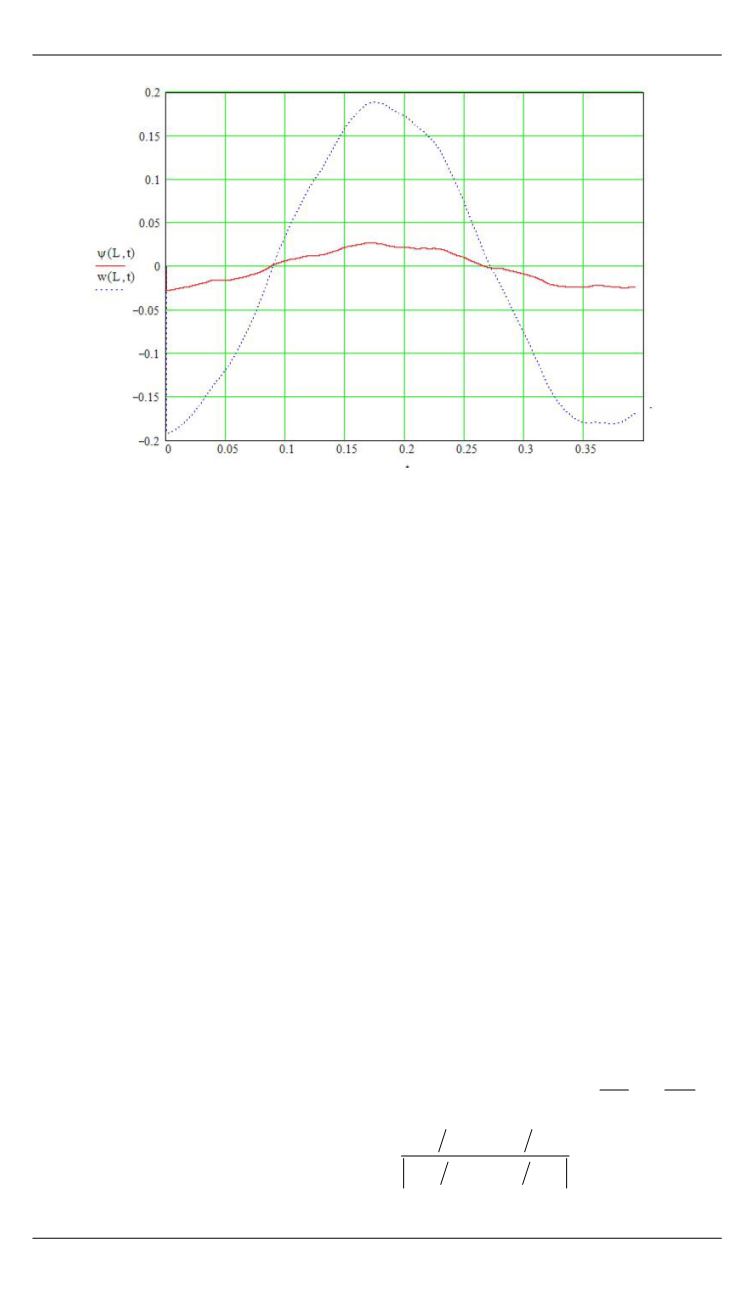
Рис. 3.
Угол поворота ψ и поперечное смещение
w
свободного торца балки
в зависимости от времени
тогда закон движения точек балки в процессе колебаний может быть
записан в следующем виде:
0 0 0
0
0
0
0 0 0
0
0
0 0 0
0
, , ,
,
,
, , ,
, ,
, , ,
.
x x y z t x
x t y
y x y z t y w x t
z x y z t z
В данном случае интересен закон движения точек боковой по-
верхности балки. Введем цилиндрические лагранжевы координаты
0
,
x
0
cos
y r
,
0
sin
z r
. Тогда закон движения точек боковой
поверхности балки (
r R
) будет описываться соотношениями
, ,
,
cos ,
, ,
cos
, ,
, ,
sin .
x
t
t R
y
t R w t
z
t R
(9)
При
const
и
const
формулы (9) дают координатные линии
на деформированной поверхности балки в текущий момент времени.
Следовательно, можно вычислить касательные векторы
r
и
r
к
этим линиям, а тогда и нормаль
r
r
n
r
r
к деформиро-
ванной поверхности в лагранжевых координатах. В частности,


