Исследование точности метода распределенной присоединенной массы …
11
производной (18) лагранжевы координаты соответствующей точки
поверхности балки фиксированы, то, пользуясь выражениями (9) и
(10), получим
ж
, , ,
, , ,
, ,
,
Т
d x
t y
t z
t
v v
d t
t
где
ж
v i
j
k
x
y
z
– скорость частиц жидкости. Компоненты
скорости жидкости на поверхности балки можно вычислить следую-
щим образом. Дифференцируя численно (17) по
s
, находим составля-
ющую скорости жидкости вдоль образующей балки
, cos
s
v
s t
s
.
Составляющая скорости в окружном направлении получается диф-
ференцированием (17) по
:
,
sin
s t
v
R
. Нормальная скорость
жидкости к поверхности балки задается соотношением (13). В каче-
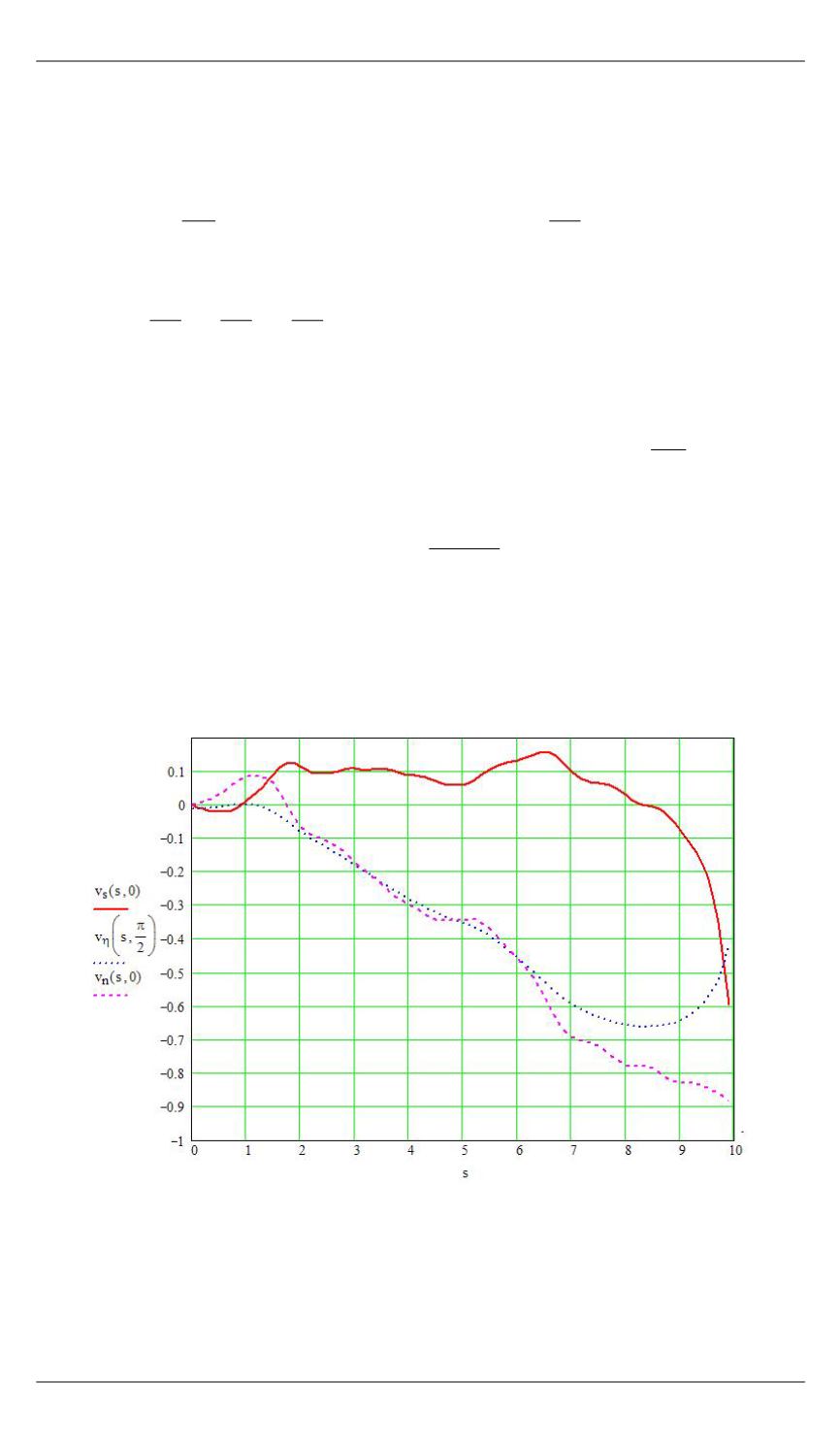
стве примера на рис. 4 приведены значения этих величин, рассчитан-
ные вдоль боковой поверхности балки для момента времени
0, 2
t
с
(см. также рис. 3).
Рис. 4.
Компоненты скорости жидкости вдоль поверхности балки
Значения скорости жидкости и точек тела оказываются на один-
два порядка меньше, чем значения производной (18). По этой причине
в формулу (16) будем подставлять в качестве частной производной по-
тенциала по времени значение (18), а также пренебрегать квадратом


