Исследование точности метода распределенной присоединенной массы …
3
Теоретически этот подход несостоятелен, как показано в работе [9]
применительно к расчету распределенной нестационарной нагрузки на
деформируемую панель оперения ЛА.
Задача данной работы – проанализировать указанный подход в
условиях поперечных упругих колебаний корпуса ЛА при выходе из
ПУ, для чего будет достаточно следующей упрощенной постановки
задачи. Рассматривается однородная балка Тимошенко кругового по-
перечного сечения, закрепленная одним концом в неограниченном
плоском экране (рис. 2). Рассчитываются поперечные колебания бал-
ки, вызванные внезапным снятием поперечной силы с ее свободного
торца. На основе заданных параметров поперечных колебаний балки
формируются граничные условия для расчета нестационарной гидро-
динамической силы на балку МГЭ в осесимметричной постановке и
МПС. По результатам сравнения расчетов делаются выводы относи-
тельно практической целесообразности подхода, основанного на ис-
кусственном «распределении» присоединенных масс вдоль корпуса
деформируемого ЛА.
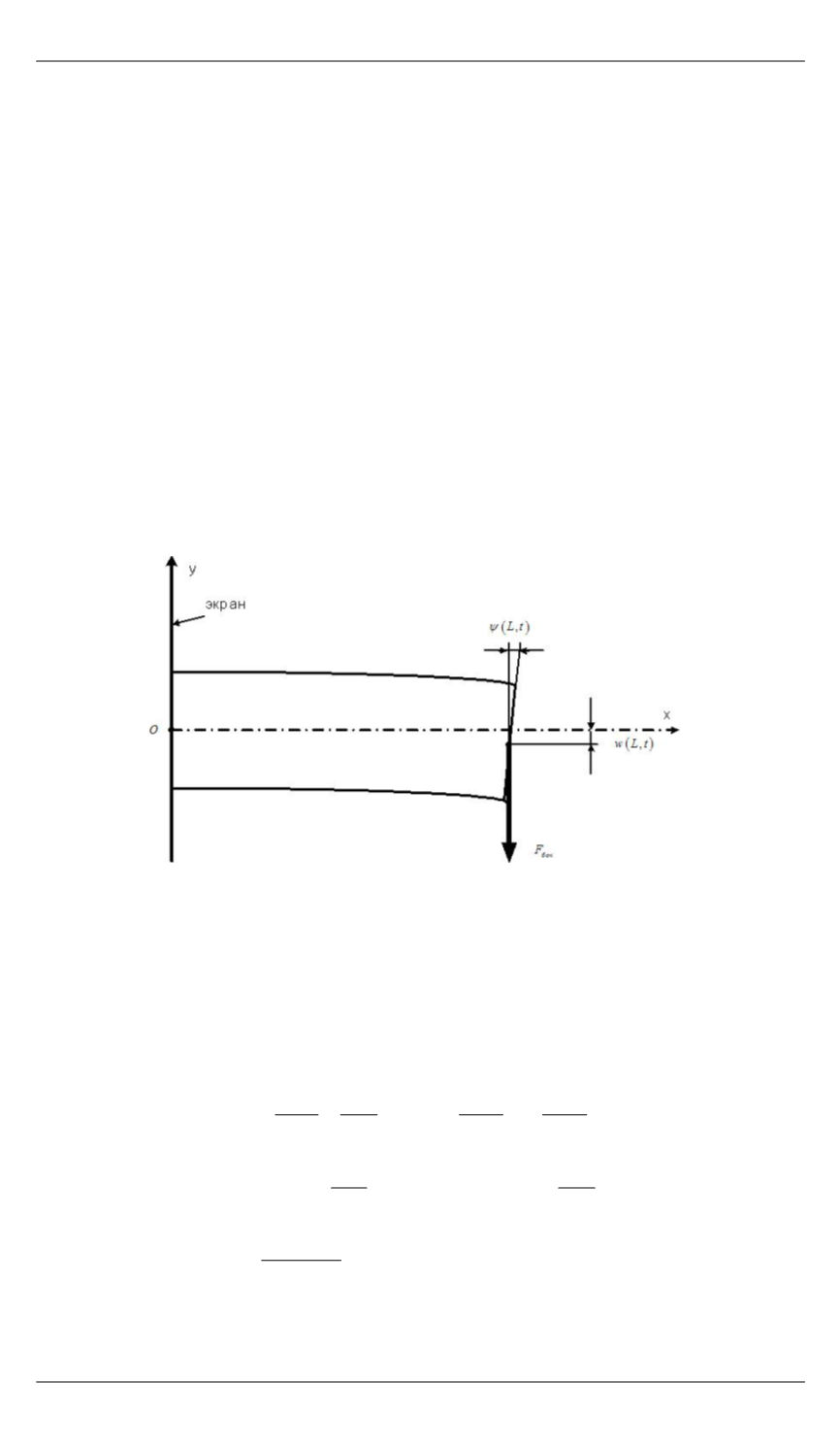
Рис. 2.
Поперечные колебания балки Тимошенко
Расчет поперечных колебаний балки Тимошенко.
Уравнения
балки Тимошенко хорошо известны [10]. Они имеют «правильный»
тип (гиперболический) и для кругового цилиндра с хорошей точно-
стью передают характер основной формы трехмерных изгибных ко-
лебаний. Имеем (см. рис. 2)
2
2
2
2
,
,
,
,
6 1
,
7 6
Т
Т
w Q
M
S
J
Q
x
x
t
t
w
Q S
M E J
x
x
(4)
где
x
– продольная координата вдоль балки;
t
– время;
w
– попе-
речное смещение сечения с координатой
x
как целого в направлении


