А.В. Плюснин
,
И.А. Доденко
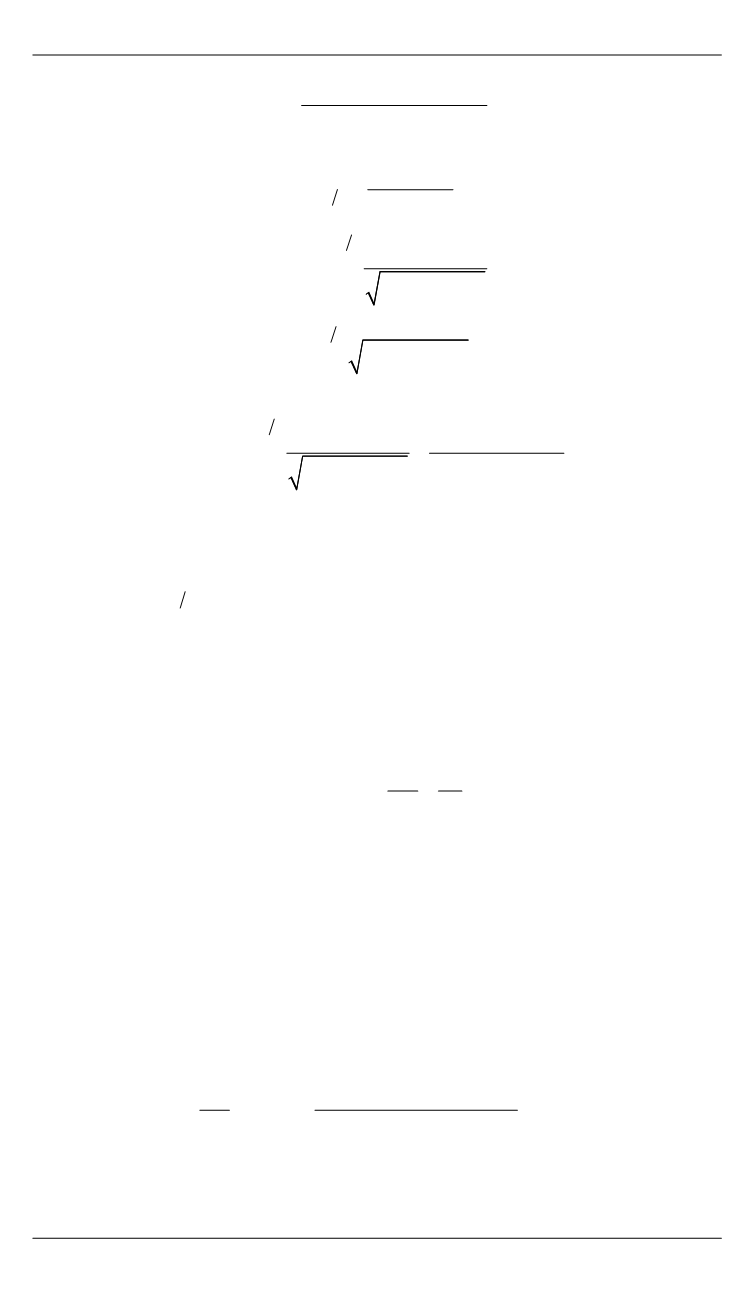
10
2
2
2
4
M
M
M
r r
k
r r
z z
,
1
1 2
2
j
j
j
,
2
2
2 2
0
1 sin
d
k
k
,
2
2
2 2
0
1 sin
k
k
d
.
2
2
2
2
2
2
2 2
0
sin
D
1 sin
k
k
d
k
k
k
.
Граничное интегральное соотношение (15) теперь легко перепи-
сать в виде системы линейных алгебраических уравнений относи-
тельно
1 2
,
j
t
и решить для ряда моментов времени стандарт-
ным прямым методом [16].
Вычисление погонной гидродинамической силы на боковую
поверхность балки.
Для определения силового воздействия жидко-
сти на колеблющуюся балку воспользуемся интегралом Коши – Ла-
гранжа [4]:
2
ж
.
2
v
p
t
(16)
Значения потенциала скоростей жидкости на поверхности балки
, ,
, cos
s t
s t
(17)
получим, решая для заданных моментов времени граничное инте-
гральное уравнение (15) относительно функции
,
s t
. Проведя рас-
четы для трех моментов времени
t
,
t
,
t
, можно получить чис-
ленным дифференцированием производную потенциала по времени:
,
,
, ,
cos .
2
s t
s t
d s t
d t
(18)
Строго говоря, производная по времени в соотношении (18) вы-
числяется для подвижной точки. Если считать, что при вычислении


