Теплопроводность текстурированного композита с анизотропными. . .
где
d
— символ Кронекера (единичный тензор второго ранга),
d
= 1
при
=
и
d
= 0
при
̸
=
. В этом случае каждая из строк матрицы
(1) задает компоненты вектора (орта)
e
в ортогональных микроосях,
а при
=
равенство (4) является условием ортогональности двух
ортов
e
и
e
. Таким образом, из девяти элементов матрицы (3)
с учетом равенства (4) независимыми будут только три. Это связано,
в частности, с тем, что любую ориентацию микроосей относительно
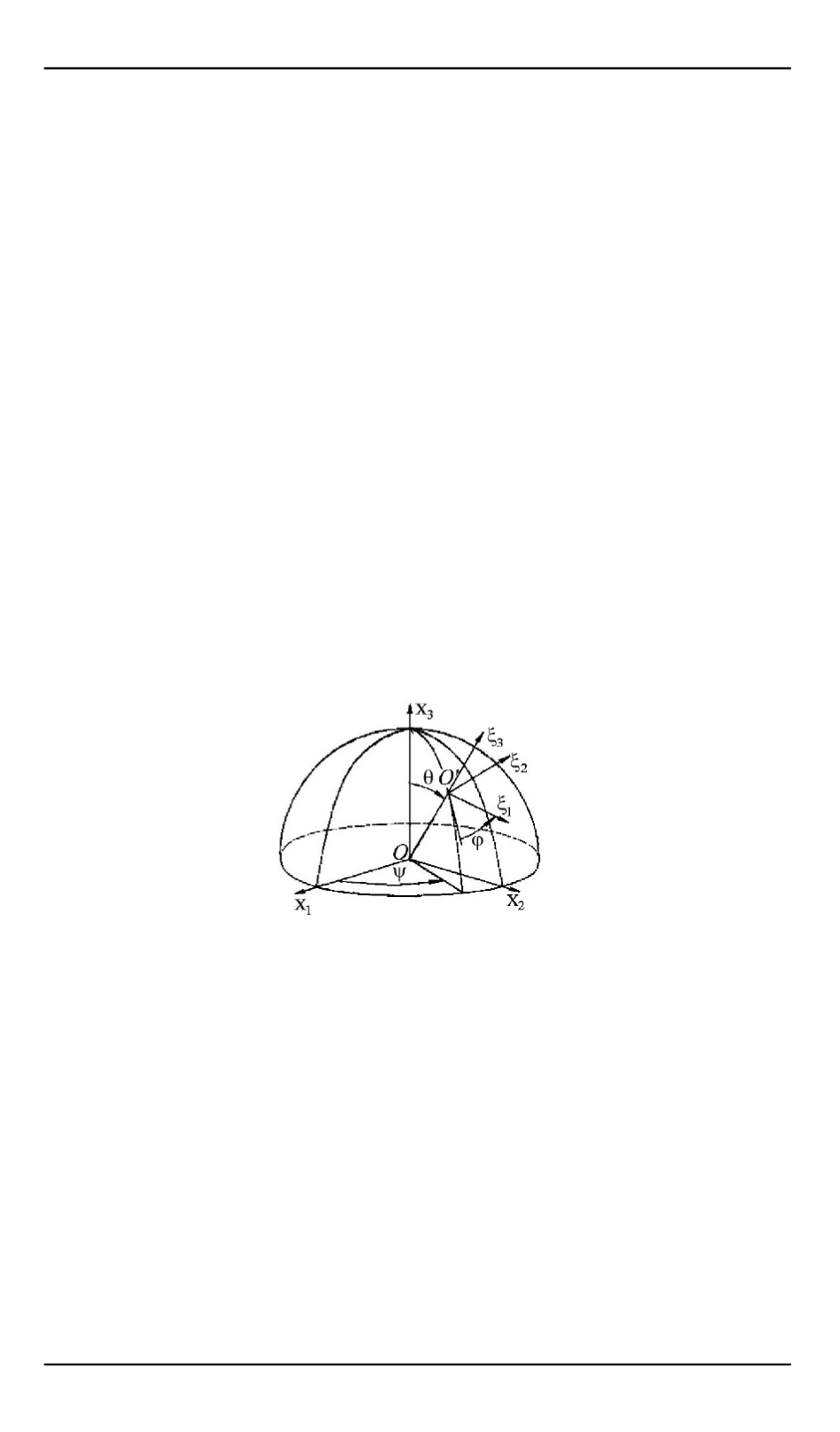
макроосей можно задать тремя угловыми координатами Эйлера: уг-
лом собственного вращения
3
, углом прецессии
y
и углом нутации
j
[4]. Углы
y
и
j
задают направление одной из микроосей (на ри-
сунке оси
′
x
3
) относительно макроосей, а угол
3
, отсчитываемый от
положения меридиана с долготой
y
на сфере единичного радиуса —
поворот репера микроосей вокруг микрооси
′
x
3
. Элементы матрицы
(3) выражают через углы Эйлера следующим образом [5]:
11
= cos
3
cos
y
cos
j
−
sin
3
sin
y
,
12
=
−
cos
3
sin
y
cos
j
−
sin
3
cos
y
,
13
= cos
3
sin
j
,
21
= sin
3
cos
y
cos
j
+ cos
3
sin
y
,
22
= cos
3
cos
y
−
sin
3
sin
y
cos
j
,
23
= sin
3
sin
j
,
31
=
−
cos
y
sin
j
,
32
= sin
y
sin
j
,
33
= cos
j
.
(5)
Ориентация микроосей симметрии относительно макроосей
Пусть расположение некоторой составной эллипсоидальной части-
цы относительно координат с макроосями
′
x
определено заданны-
ми значениями углов Эйлера
3
,
y
и
j
. По компонентам
l
o
11
=
l
o
1
,
l
o
22
=
l
o
2
и
l
o
33
=
l
o
3
тензора эффективной теплопроводности этой ча-
стицы в микроосях найдем компоненты
l
*
(
= 1
,
2
,
3
) этого тензора
в макроосях c использованием элементов транспонированной матри-
цы и соотношений [5]
l
*
=
l
o
,
= 1
,
2
,
3
.
(6)
В соответствии с формулой (6) запишем
l
*
11
=
l
o
1
2
11
+
l
o
2
2
21
+
l
o
3
2
31
,
(7)
l
*
22
=
l
o
1
2
12
+
l
o
2
2
22
+
l
o
3
2
32
,
(8)
3


