Д.А. Крылов, Н.И. Сидняев, А.А. Федотов
2
нечности будем считать однородным с постоянным вектором скоро-
сти
V
, параллельным оси
1
x
и направленным в положительную
сторону этой оси. Пусть закон движения крыла имеет вид
1 2
, , ,
k
k
s
s s s
x x a a t
1
0
1,
s
a
2
1
1,
s
a
(1)
где
k
s
x
и
l
s
a
( 1, 2, 3 ;
k
1, 2)
l
— соответственно декартовы и ла-
гранжевы координаты точек крыла на поверхности;
t
— время.
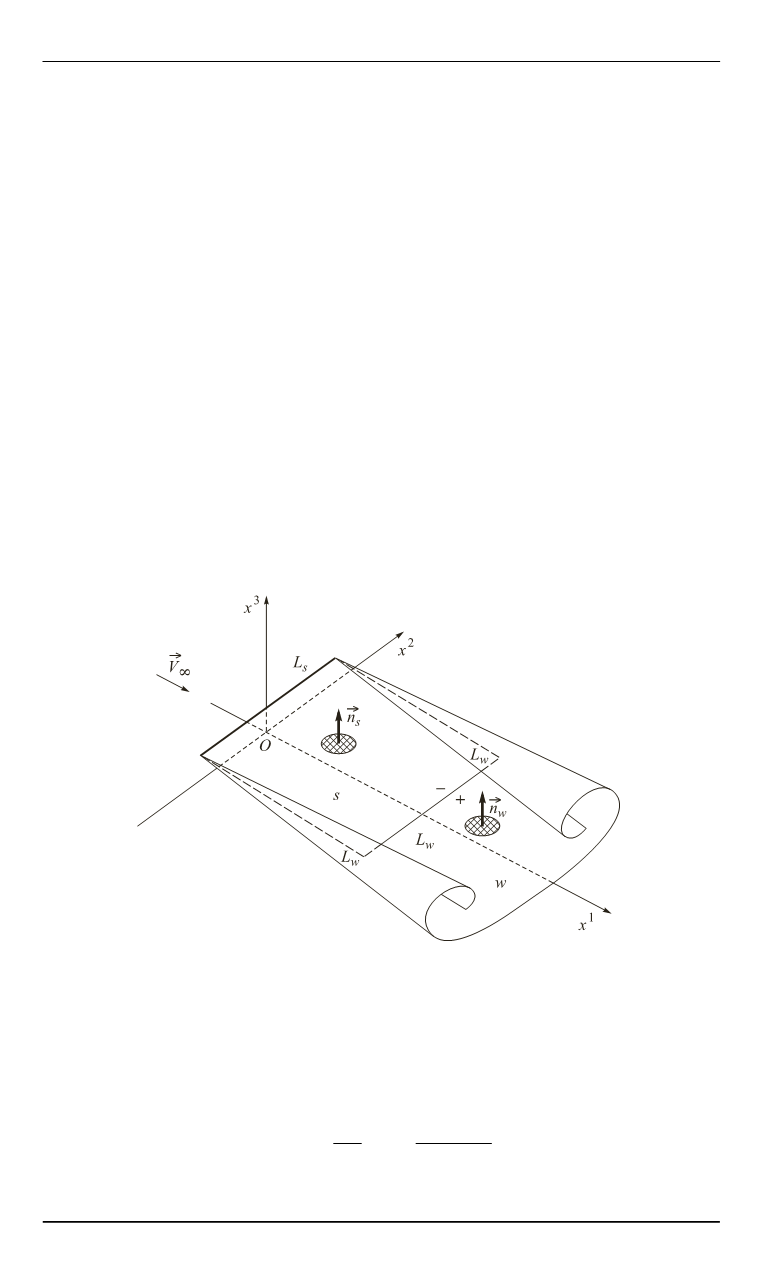
Полагаем, что бесконечно тонкое крыло схематизирует собой ре-
альное крыло, имеющее обтекающуюся без отрыва потока закруг-
ленную кромку
s
L
и острую кромку
w
L
, с которой в поток жидкости
плавно стекает вихревой след, возникающий за крылом при его дви-
жении. Поэтому считаем, что крыло является несущей поверхностью
с передней кромкой
1
(
0,
s
a
2
1
1),
s
a
обтекаемой без отрыва, на
которую действует подсасывающая сила [1]. С задней
1
(
1
s
a
,
2
1
1)
s
a
и боковой
1
(0
1,
s
a
2
1)
s
a
кромок в поток стекает
свободная вихревая поверхность. Передняя кромка является кромкой
натекания
s
L
, а задняя и боковая — кромками стекания
w
L
(рис. 1).
Рис. 1. Схема обтекания крыла
Скорости
,
k
k
v
V e
индуцируемые несущей (
)
s
и свобод-
ной вихревой (
)
w
поверхностями в точке наблюдения с радиус-
вектором
r
в момент времени
,
t
вычисляют по формуле [2]
1 2
3
1
( , )
.
4
q l
p l
t
da da
R
R
V V r
(2)


