
Групповое применение беспилотных планирующих летательных аппаратов
Инженерный журнал: наука и инновации
# 11·2017 7
ТИ смещена относительно оси симметрии проекции назначен-
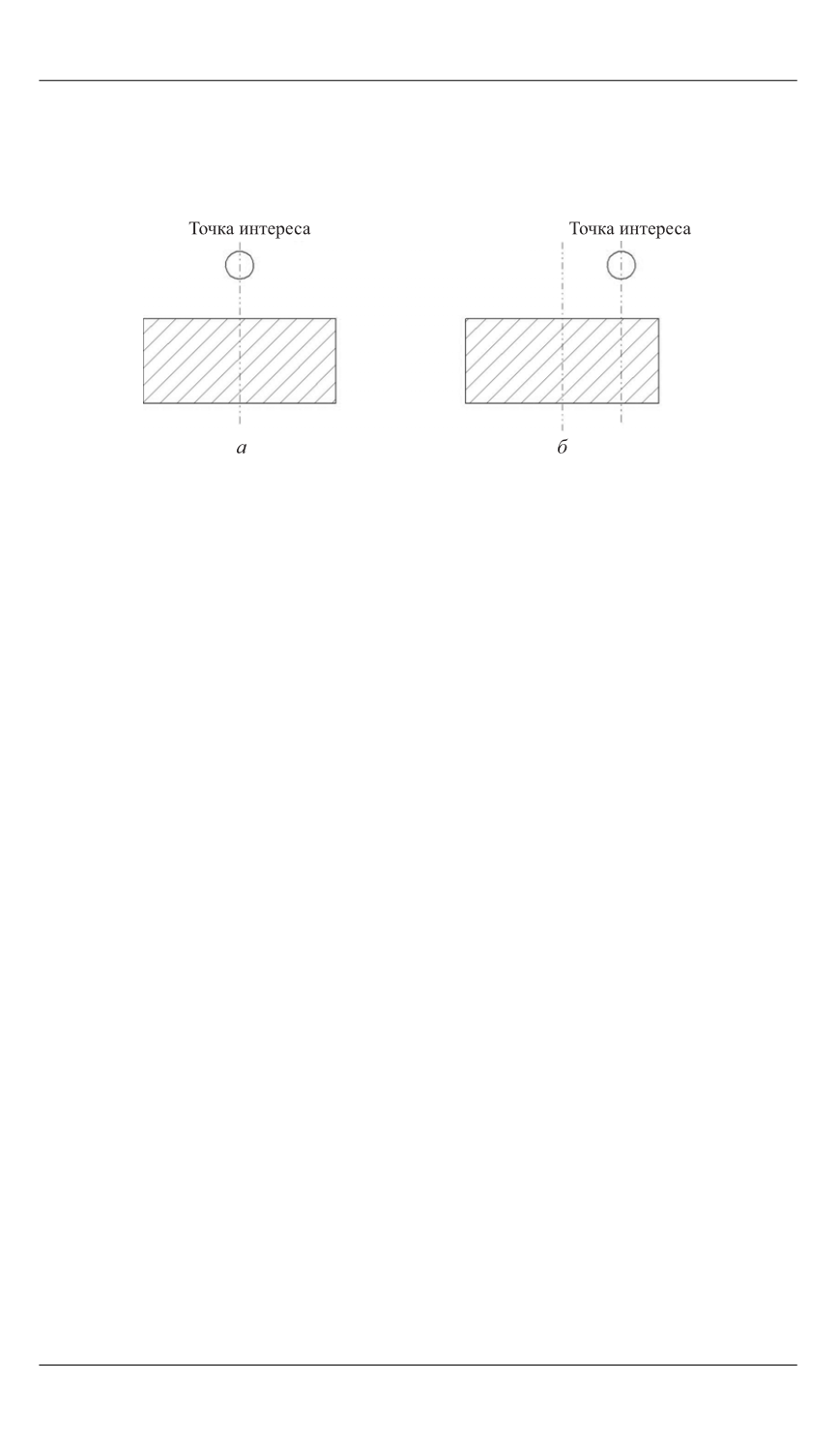
ного параллелепипеда; облетать препятствие необходимо со стороны,
находящейся ближе к ТИ.
Рис. 5.
Возможные варианты облета препятствия:
а
— ТИ находится на оси симметрии назначенного прямоугольни-
ка;
б
— ТИ смещена относительно оси симметрии назначенного
прямоугольника
Построение траекторий полета, как и в Задаче 1, осуществляется
с помощью назначения навигационных точек с той лишь разницей,
что для облета препятствия необходимо строить траектории с использо-
ванием как минимум двух навигационных точек
N
i
1
(
X
gi
1
,
Z
gi
1
) и
N
i
2
(
X
gi
2
,
Z
gi
2
),
i
= 1, …,
n
для каждой
i
-й траектории каждого
i
-го БПК ЛА.
Пусть носитель движется в направлении ТИ по некоторой прямо-
линейной траектории с углом τ = 0. В отличие от Задачи 1 базовая
траектория
L
б
— виртуальная, т. е. аппарат не может совершать полет
по этой траектории, и она является вспомогательной, относительно
которой будут строиться другие
i
-е траектории.
Выбор каждой НТ осуществляется следующим образом.
1. Для каждой траектории зафиксируем значение координат
навигационной точки по оси
OX
g
. Они будут равны координатам
X
g
вершин заданного прямоугольника (рис. 6).
2. Координаты
Z
g
для обеих навигационных точек каждой
i
-й тра-
ектории будут равны. Как и в задаче 1 выбор значения координаты
Z
g
осуществляется путем ее перебора c шагом Δ
Z
g
= 50 м.
Некоторые результаты моделирования.
Проводя аппроксима-
цию по найденным координатам
Z
g
, получаем функциональные зави-
симости
Z
g
=
f
(
t
i
,
V
0
,
H
0
, Δ, ε), с помощью которых можно рассчитать
координаты навигационных точек для любого БПК ЛА заданной
аэродинамической схемы, стартующего в любой момент времени
[
]
1
,
∈
n
t t t
(рис. 7).
















