
В.Т. Грумондз, Е.И. Карпежников, М.А. Полищук
6
Инженерный журнал: наука и инновации
# 11·2017
Разработанный алгоритм справедлив для ограничений, установ-
ленных в постановке задачи 1. На практике возникает множество до-
полнительных факторов, влияющих на работу алгоритма, например,
особенности рельефа земной поверхности – естественные (складки
местности, горы) и искусственные (здания, инженерные сооружения)
преграды. В этих случаях для достижения группой точки интереса
необходимо построить траектории с учетом расположения препят-
ствия на пути полета группы.
Постановка задачи 2
. Предположим, что точка интереса скрыта
за препятствием. Координаты препятствия и ТИ известны. Необхо-
димо разработать алгоритм облета препятствия и одновременного
сбора в ТИ всех БПК ЛА, стартующих с носителя.
Требуется для каждого
i
-го аппарата выбрать траекторию полета,
удовлетворяющую условиям Задачи 1 и дополнительным условиям,
связанным с наличием препятствия.
Алгоритм решения.
Рассмотрим случай τ = 0, препятствие пред-
ставим как бесконечный по высоте прямоугольный параллелепипед.
Такая форма позволит учесть большинство возможных препятствий
как искусственных, так и естественных.
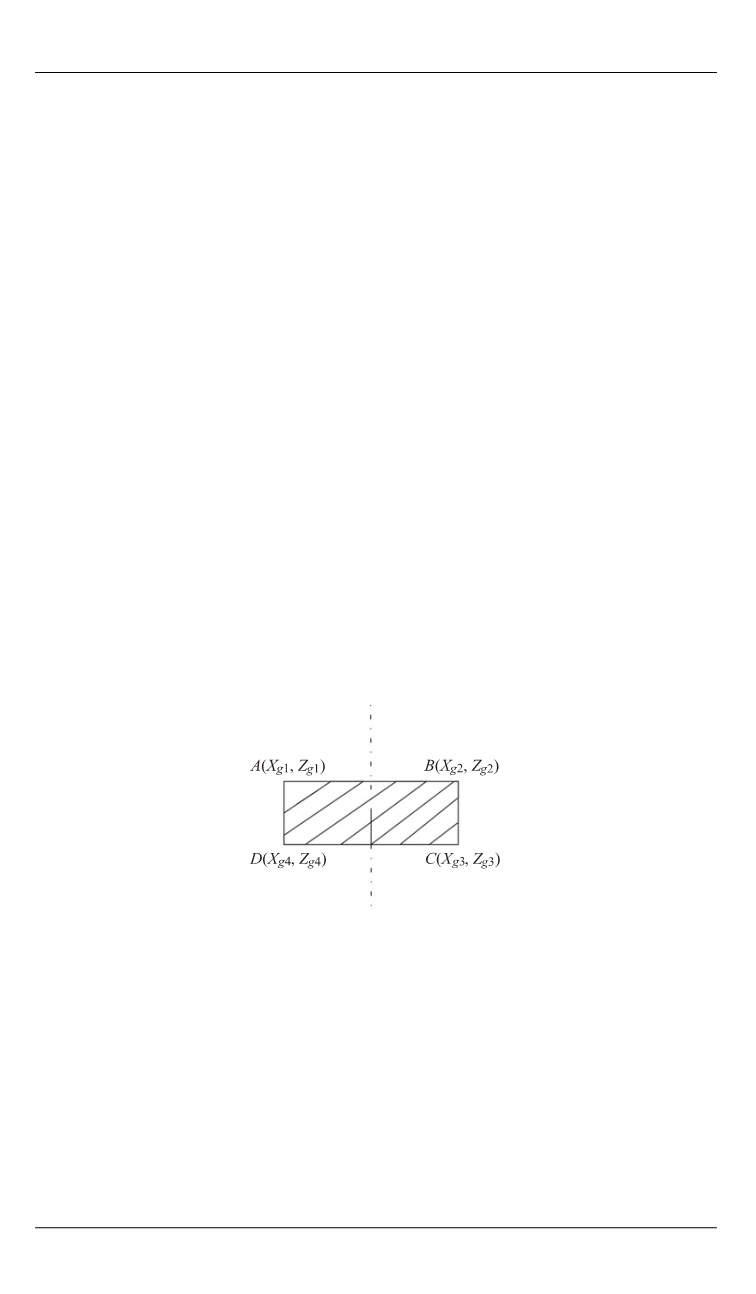
Проекцией препятствия на горизонтальную плоскость является
прямоугольник некоторой площади. Обозначим вершины этого пря-
моугольника как точки с координатами
A
(
X
g
1
,
Z
g
1
),
B
(
X
g
2
,
Z
g
2
),
C
(
X
g
3
,
Z
g
3
),
D
(
X
g
4
,
Z
g
4
) (рис. 4).
Рис. 4.
Проекция препятствия на
горизонтальную плоскость
Поскольку препятствие выбрано бесконечным по высоте прямо-
угольным параллелепипедом, возможно совершать его облет только
слева или справа. В зависимости от взаимного расположения препят-
ствия и ТИ можно выделить два варианта облета (рис. 5):
ТИ находится на оси симметрии проекции назначенного парал-
лелепипеда на горизонтальную плоскость; облетать препятствие
можно с любой стороны или с двух сторон одновременно;
















