
Сравнительный анализ напряжений
…
Инженерный журнал: наука и инновации
# 10·2017 11
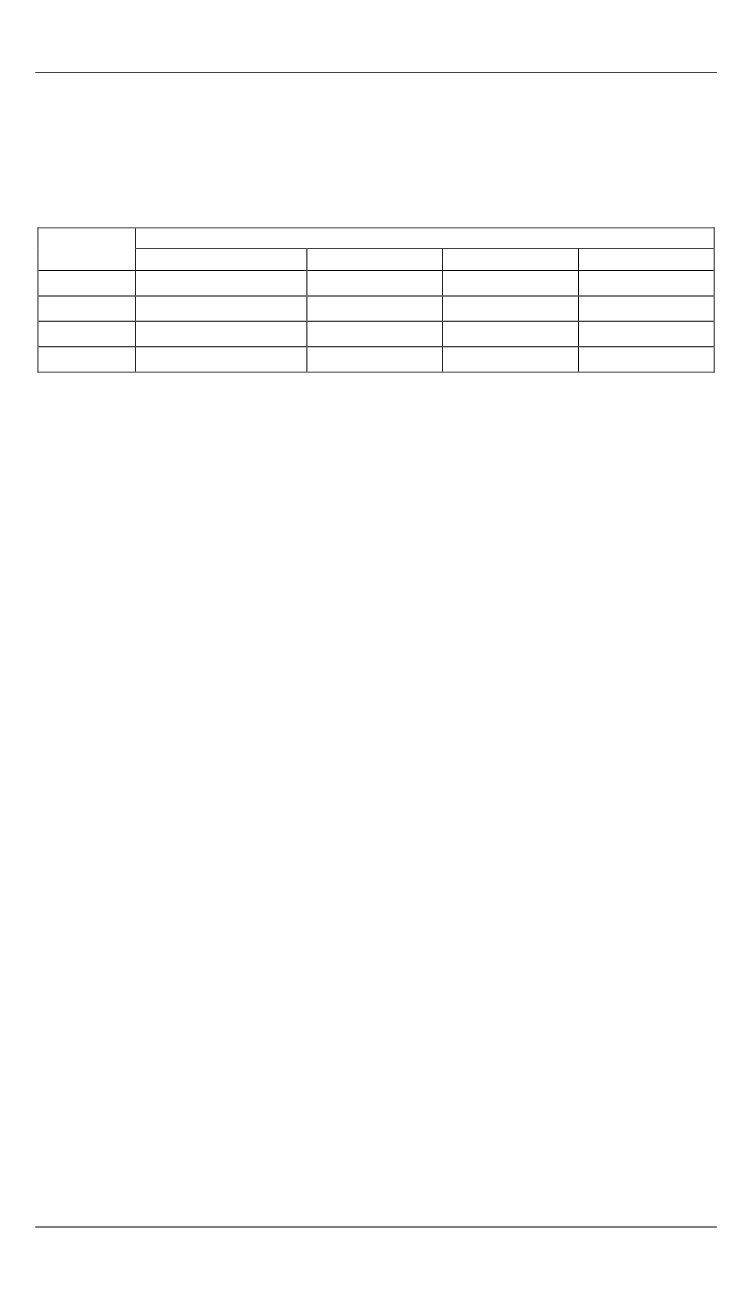
Отклонение для опорных сечений, рассчитанное по формуле (21),
приведено в табл. 2.
Таблица 2
Относительное отклонение компонент тензора напряжений, рассчитанных
по асимптотической и трехмерной теориям в опорных сечениях
σ
ij
x
1
0,125
0,25
0,375
0,5
σ
11
0,528
2,59
0,448
0,364
σ
22
2,779
3,059
2,647
0,452
σ
13
0,066
0,065
0,065
–
σ
33
0,021
0,012
0,013
0,009
Согласно формуле (20), компонента тензора напряжений
13
σ
,
рассчитанная по АТ, в центральном сечении обращается при
1
0,5
=
x
в нуль. Численное решение, полученное на основе трехмерной тео-
рии (см. рис. 5,
г
), отражает близость к решению на основе асимпто-
тической теории.
Результаты сравнения решений, полученных по асимптотической и
трехмерной теориям, показывают, что АТ обеспечивает достаточно вы-
сокую точность для всех напряжений. Наибольшая точность достигает-
ся для поперечных и сдвиговых напряжений, наименьшая — для боко-
вых нормальных напряжений
22
σ
. Тем не менее эта точность довольно
высока — относительная ошибка не превышает 3 %, что является хо-
рошим результатом для относительно короткой пластины (малый пара-
метр 0,025). Точность расчетов повышается при стремлении малого па-
раметра к нулю, т. е. для еще меньших значений
.
κ
Таким образом, как и для симметричной пластины [12], разрабо-
танный метод позволяет получать довольно точные решения и для
несимметричных пластин.
Заключение.
Проведенный сравнительный анализ распределений
напряжений в несимметричных многослойных пластинах, вычисленных
на основе асимптотической теории и трехмерного конечно-элементного
расчета, позволяет сделать вывод о том, что асимптотическая теория
обладает значительными преимуществами в сопоставлении с трехмер-
ным конечно-элементным методом решения задач для тонкостенных
многослойных пластин: при использовании ее требуются значительно
менее мощные вычислительные средства и существенно меньшее ма-
шинное время для достижения одинаковой точности расчетов.
ЛИТЕРАТУРА
[1]
Григолюк Э.И., Куликов Г.М. Обобщенная модель механики тонкостенных
конструкций из композитных материалов.
Механика композитных мате-
риалов
, 1988, № 4, с. 698–704.
















