
Моделирование калибровки динамически настраиваемых гироскопов…
Инженерный журнал: наука и инновации
# 10·2017 7
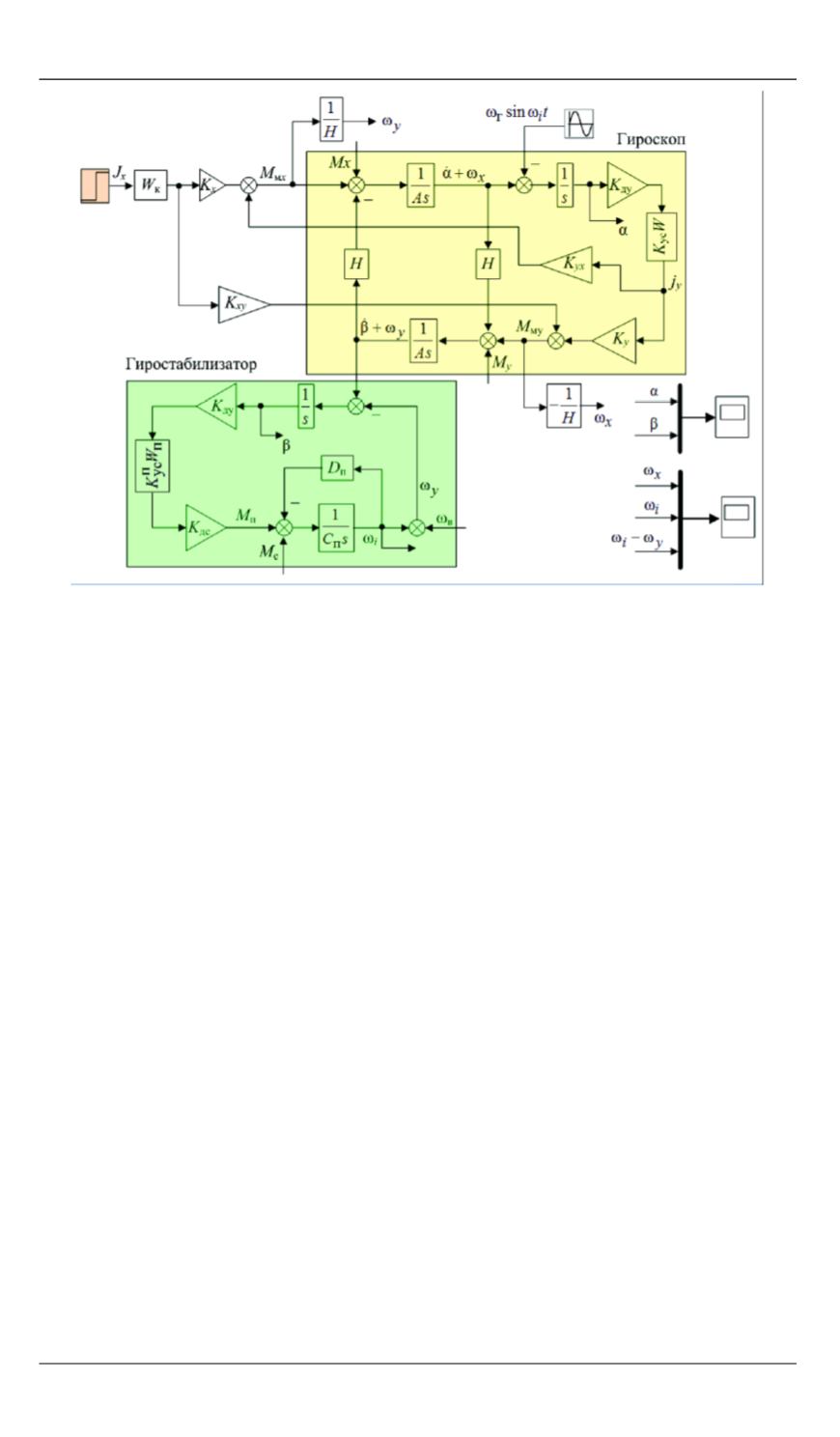
Рис. 5.
Структурная схема системы гироскоп — гиростабилизатор для положения 1
При моделировании использовали следующие исходные данные:
•
параметры ДНГ типа МГ-4 [4] —
A
= 5·10
–7
H·м·с
2
,
H
=
= 1,4·10
–3
H·м·с,
K
ду
= 6,0 В/рад;
•
параметры стенда —
С
п
= 0,04 H·м·с
2
,
D
п
= 0,01H·м·c.
Для этих параметров стенда и гироскопа по результатам модели-
рования определены параметры КОС, обеспечивающие достаточные
запасы устойчивости и качество переходных процессов:
•
для ДНГ —
K
ус
= 12 A/В,
K
x
= 1,4·10
–2
H·м/A,
K
xy
=
= 1,3·10
–3
H·м/A,
M
x
=
M
y
= 0,
K
y
= 1,7·10
–2
H·м/A,
K
yx
= 1,6·10
–3
H·м/A,
T
1
= 0,015 c,
T
2
= 0,001 c;
•
для стенда —
п
ус
K
= 4 A/В,
K
дс
= 1 H·м/A,
T
с1
=
T
с2
= 0,08 с,
T
с3
=
= 0,008 с.
На рис. 6 представлены результаты моделирования движения ро-
тора гироскопа и платформы при заданной максимальной угловой
скорости ротора гироскопа ω
y
= 150 град/с. Видно, что через 3 с по-
сле подачи тока управления переходной процесс практически завер-
шается. Также из графиков следует, что установившееся значение
угловой скорости ротора ДНГ ω
x
практически равно нулю, так как
значения, соответствующие собственному дрейфу гироскопа, а также
горизонтальной и вертикальной проекции собственного вращения
Земли ничтожно малы на фоне задаваемой угловой скорости стенда.
Угловая скорость платформы ω
i
также практически равна угловой
скорости прецессии ротора гироскопа ω
y
по вертикальной оси.
















