Алгоритм нахождения траектории перелета между двумя эллиптическими орбитами

9 / 11

Алгоритм нахождения траектории перелета между двумя эллиптическими орбитами
Инженерный журнал: наука и инновации # 6·2017 9
зительно равными 90°. Фактически траектория, по которой КА со-
вершает движение между плоскостями, будет представлять дугу.
Примем 0,0134   рад (0,768°), 28 000 
C v м/с. Тогда, согласно
уравнению (23), 375, 2  v м/с. Длину дуги можно вычислить,
умножив  на средний радиус орбиты 1
Mid
1 2 10   r м, в результате
вычислений получим 2,68·109 м. Разделив длину дуги на скорость,
получим время перехода между плоскостями — 82,67 сут. Разделив
скорость на интервал времени, получим ускорение — 5,25·10 –5 м/с2.
Нормальное ускорение аN можно также найти по известной тео-
реме об изменении момента количества движения: производная по
времени от кинетического момента механической системы относи-
тельно некоторого неподвижного центра равна геометрической сум-
ме моментов всех внешних сил, действующих на систему, относи-
тельно того же центра (рис. 5) [3]:
 
   N
dK d d
K Fr a v
dt dt dt
, (24)
где F — сила, действующая на тело и перпендикулярная плоскости
орбиты.
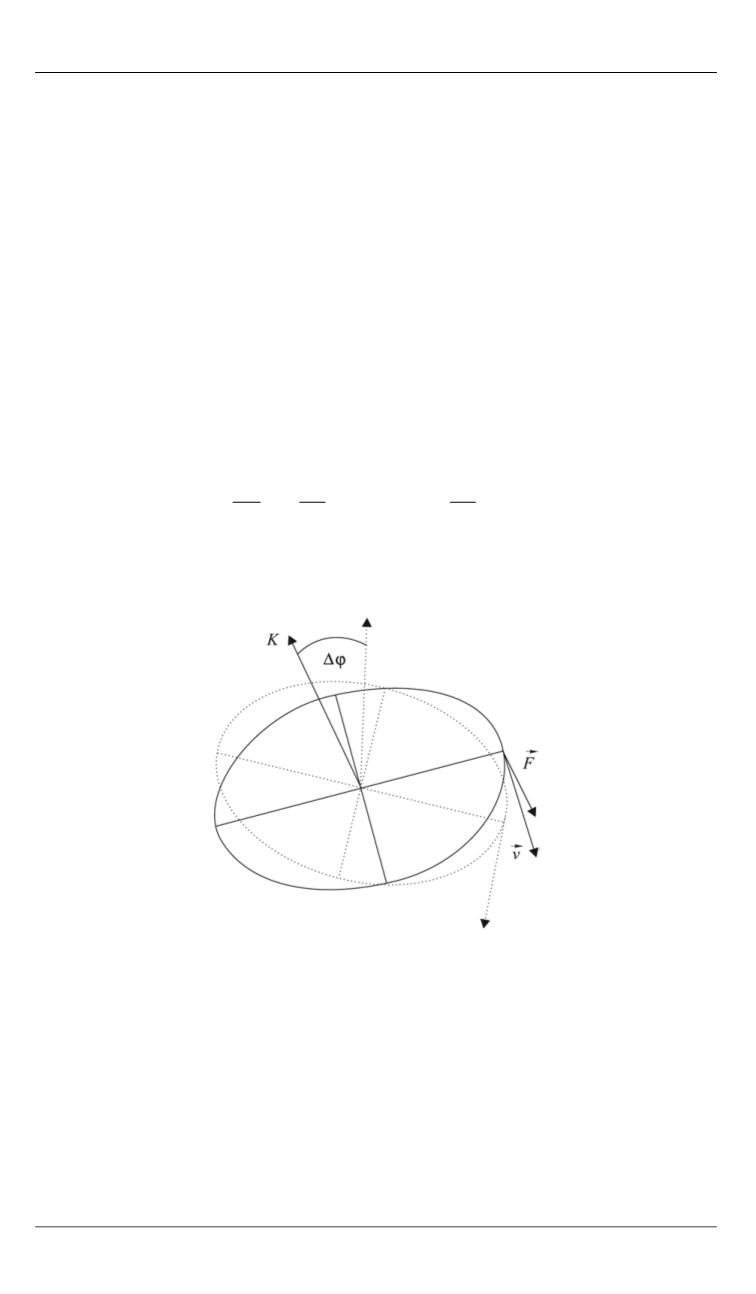
Рис. 5. Изменение плоскости орбиты
Приняв 0,0134   рад, 82,67  t сут (7,14·106 с), 28 000 
C v м/с,
получим 5 5,25 10   
N a м/с2.
Известно, что прецессионное движение гироскопа является без-
ынерционным, т. е. оно прекращается при исчезновении внешней си-
лы, его вызвавшей [9]. Поворот плоскости орбиты небесного тела
при сохранении его углового момента, логично также рассматривать
как безынерционное движение.