
Н.В. Островский
8
Инженерный журнал: наука и инновации
# 6·2017
Таблица 3
Скорости торможения для различных эллиптических перелетных орбит
,
a
м·10
11
,
C
v
м/с
,
R
v
м/с
,
C
v
м/с
,
R
v
м/с
,
v
м/с
1,9
22 007
3101
2570
–866
2712
2,0
22 222
5710
2355
–3475
4198
2,3
22 684
9976
1893
–7741
7969
3,0
23 198
14 555
1379
–12 320
12 397
Главный вывод, который необходимо сделать по данным табл. 2
и 3, состоит в том, что с увеличением эксцентриситета перелетной
орбиты значительно увеличивается радиальная скорость как в точке
отлета, так и в точке прилета, так что целесообразно использовать
эллиптическую орбиту с минимально возможным эксцентриситетом.
Для перехода КА на планетоцентрическую орбиту нет необходи-
мости нацеливать КА точно на планету и доводить его кинетические
параметры до параметров планеты.
Изменение плоскости орбиты.
Рассмотренный выше алгоритм
был найден для случая, когда исходная и конечная орбиты КА лежат
в одной плоскости. Для изменения плоскости орбиты необходимо
придать КА дополнительное ускорение, перпендикулярное плоскости
орбиты [1]. При этом величина изменения вектора скорости может
быть вычислена по уравнению:
2 sin 2
v v
,
(23)
где
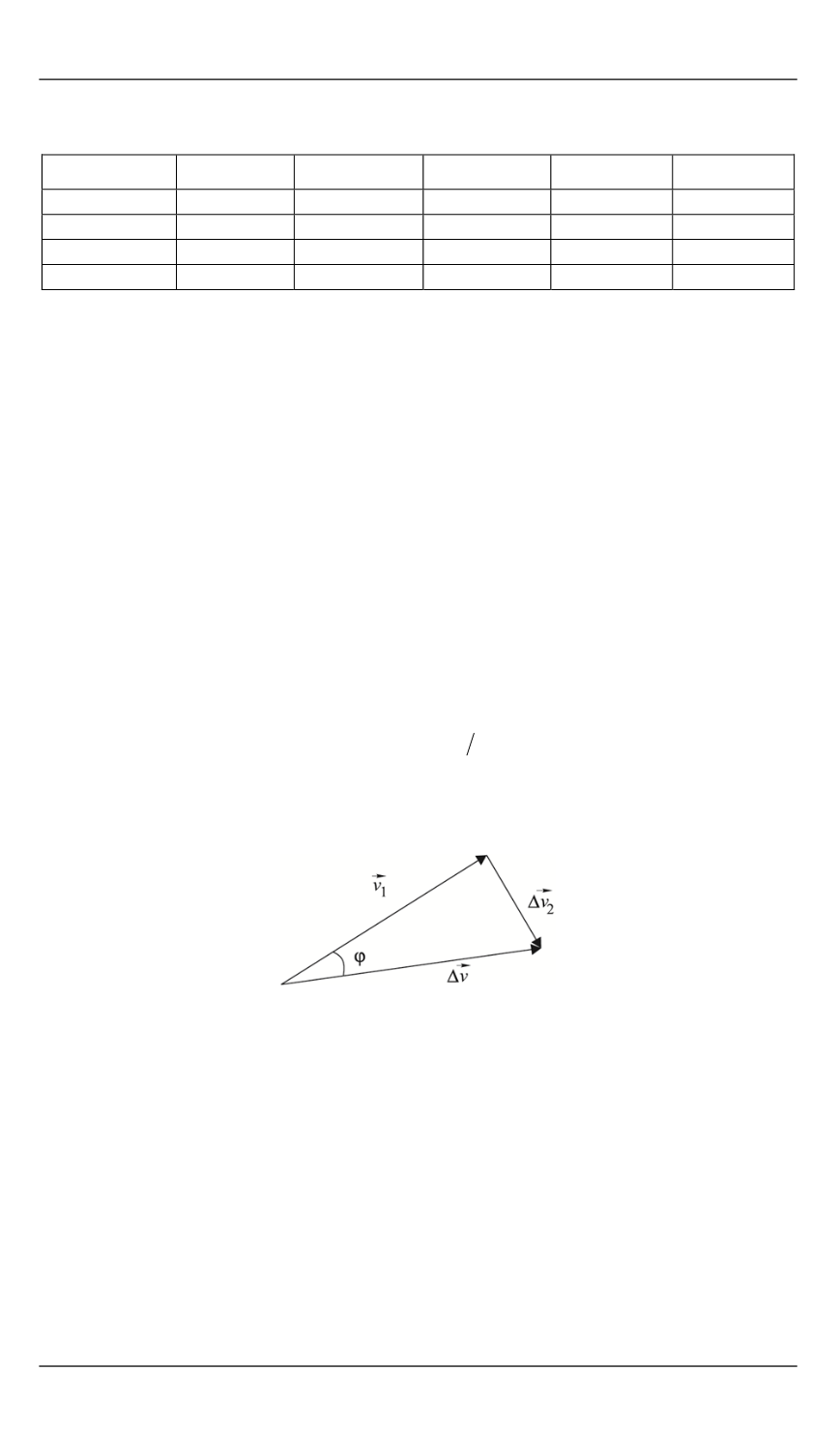
— угол, на который нужно повернуть плоскость орбиты (рис. 4).
Рис. 4.
Изменение направле-
ния движения КА:
1
v
— начальное направление вектора
скорости;
2
v
— конечное направление
после поворота на угол
Ускорение, нормальное к плоскости орбиты, должно менять не
величину вектора круговой скорости, а только его направление.
Уравнение (23) справедливо для равностороннего треугольника. Ко-
нечно, прямоугольный треугольник не может быть равносторонним,
но если
0
v
, то два прилегающих угла можно принять прибли-
















