
Н.В. Островский
2
Инженерный журнал: наука и инновации
# 6·2017
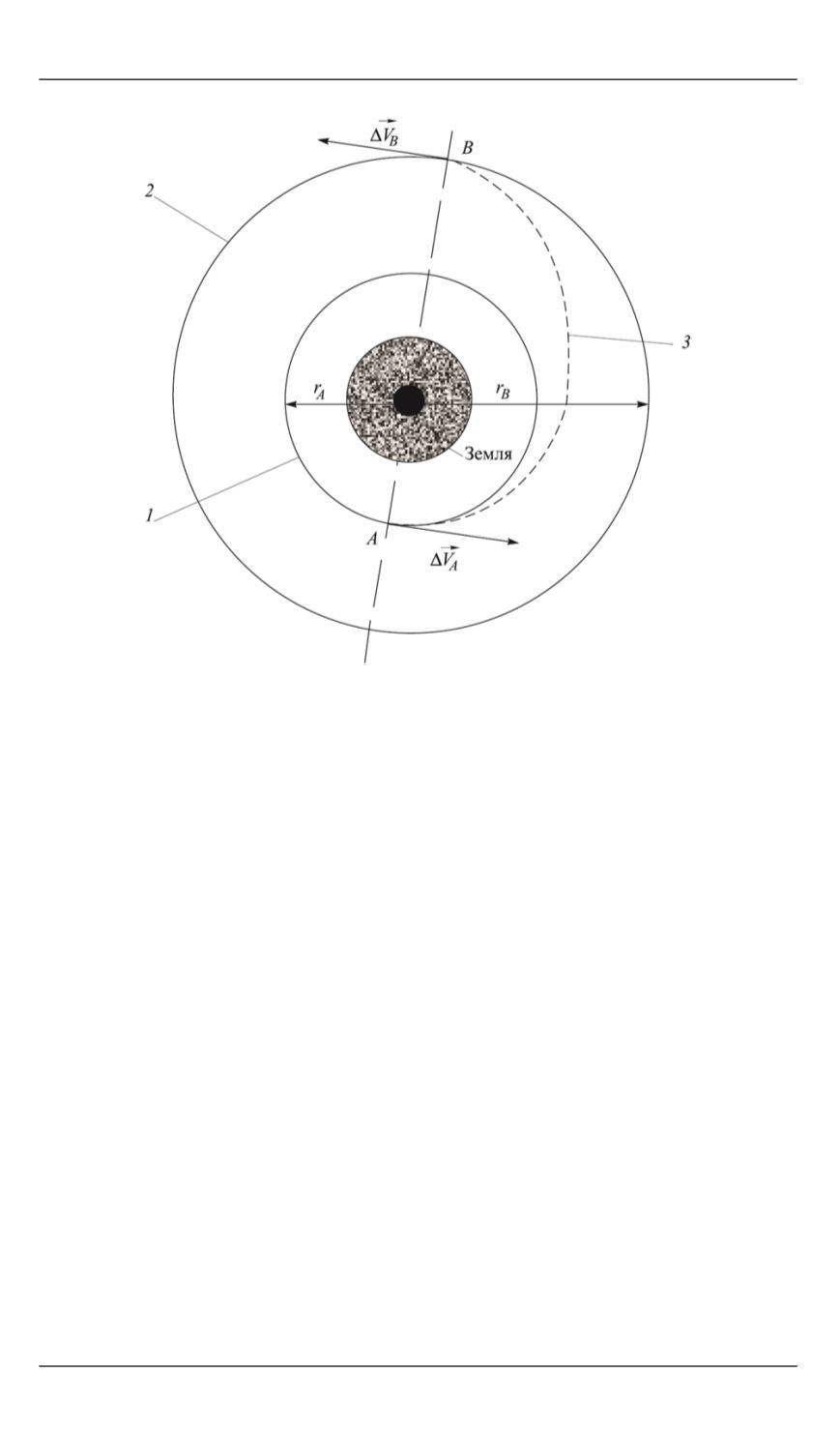
Рис. 1.
Гомановская орбита для перелета с одной круговой
орбиты на другую компланарную круговую орбиту [1]:
1
— начальная орбита;
2
— конечная орбита;
3
— гомановская орбита для перелета
Более сложная задача заключается в построении эллиптической
орбиты для перелета между двумя эллиптическими орбитами. Алго-
ритм нахождения такой орбиты в общедоступных средствах инфор-
мации отсутствует [1, 2].
Главная цель данной статьи — построить алгоритм вычисления
параметров эллиптической орбиты в зависимости от расположения
точек отлета и прилета на исходной и конечной орбитах. Найдя гео-
метрические параметры орбиты, можно вычислить свойственные ей
параметры движения КА, а на их основе — скорости разгона и тор-
можения.
Методы решения задач.
Построение перелетной эллиптической
орбиты сводится к нахождению формы эллипса, одна точка (точка
B
)
которого находится на 1-й эллиптической орбите, а другая (точка
С
) —
на 2-й (рис. 2). Причем все три эллипса имеют общий фокус
А
.
Решение данной задачи было найдено с использованием извест-
ных свойств эллипса и треугольника (теорема косинусов).
















