
Алгоритм нахождения траектории перелета между двумя эллиптическими орбитами
Инженерный журнал: наука и инновации
# 6·2017 5
Величина круговой скорости связана с длиной радиус-вектора
через
:
K
( )
( ) ( )
C
v t
K m t r t
=
.
(10)
Данная система уравнений не имеет аналитического решения, по-
этому был использован метод численного интегрирования. Расчеты
проведены с шагом
60
t
Δ =
c. Эфемериды Земли и Марса были
найдены по программе Planeph 4.2 [7].
Алгоритм нахождения параметров перелетного эллипса.
Эл-
липс однозначно можно описать любыми двумя из перечисленных
параметров [5]:
длина большой полуоси
a
;
длина малой полуоси
b
;
половина фокусного расстояния
c
;
эксцентриситет эллипса
e
.
Данные параметры связаны между собой следующими уравнени-
ями:
2 2 2
a b c
= +
;
(11)
2
2
1
c
b
e
a
a
= = −
.
(12)
Итак, нам известны длины
АВ
и
АС
и угол
ВАС
. Через точки
В
и
С
можно провести целую группу эллипсов, характеризующихся
определенной взаимосвязью параметров. Иными словами, можно,
например, найти
е
как функцию от
а
(рис. 3).
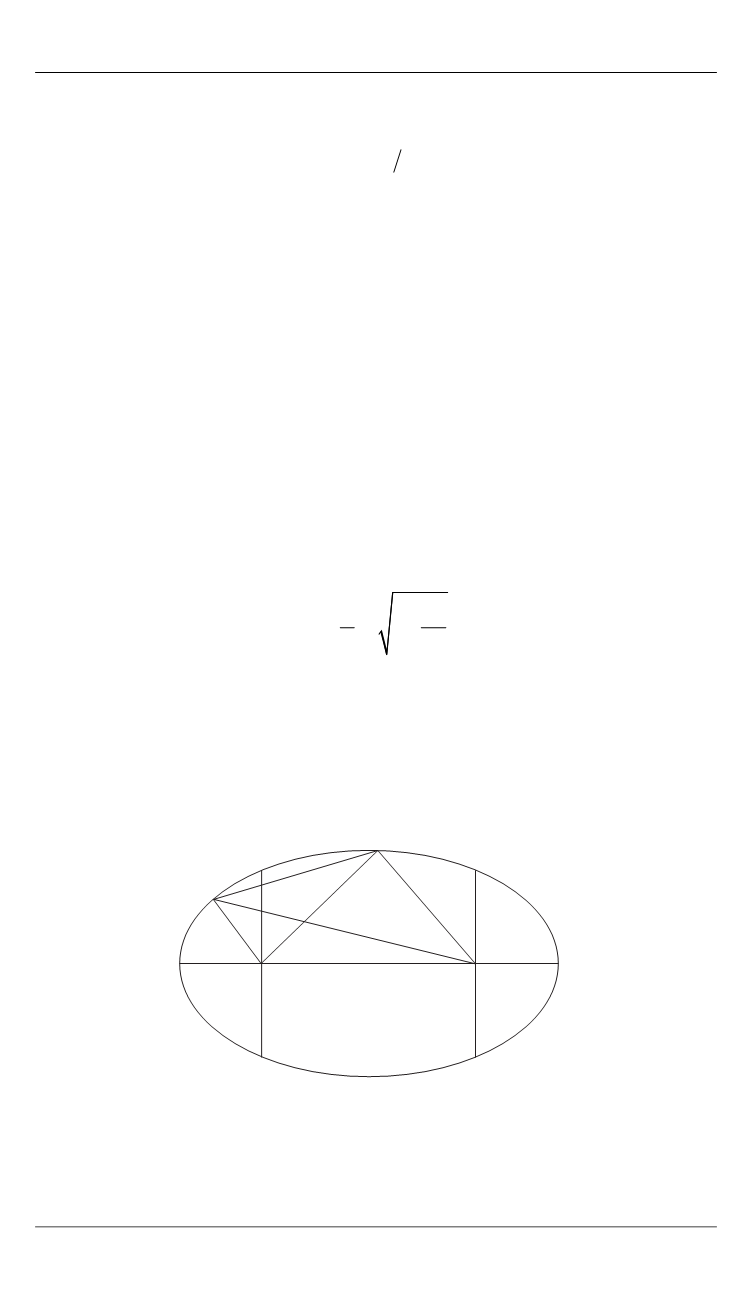
Рис. 3.
Чертеж для нахождения параметров эллипса
Выделим 2-й фокус эллипса
D
. Теперь, исходя из свойств эллипса
и треугольника, можно составить систему уравнений:
B
A
C
E
F
D
















