
С.А. Берестова, Н.П. Копытов, Е.А. Митюшов
6
Инженерный журнал: наука и инновации
# 7·2017
6 —
0, 5, 0, 5, 0, 5, 0, 5 ;
7 —
0, 5, 0, 5, 0, 5, 0, 5 ;
8 —
0,5, 0, 5,
0, 5, 0, 5 ;
9 —
0, 5, 0, 5, 0, 5, 0, 5 ;
10 —
0, 5, 0,5, 0,5,
5 0, ;
11 —
0, 5, 0, 5, 0,5, 0,5 ;
12 —
0, 5, 0, 5, 0, 5, 0, 5 .
По этим
кватернионам могут быть построены 12 положений объекта, равно-
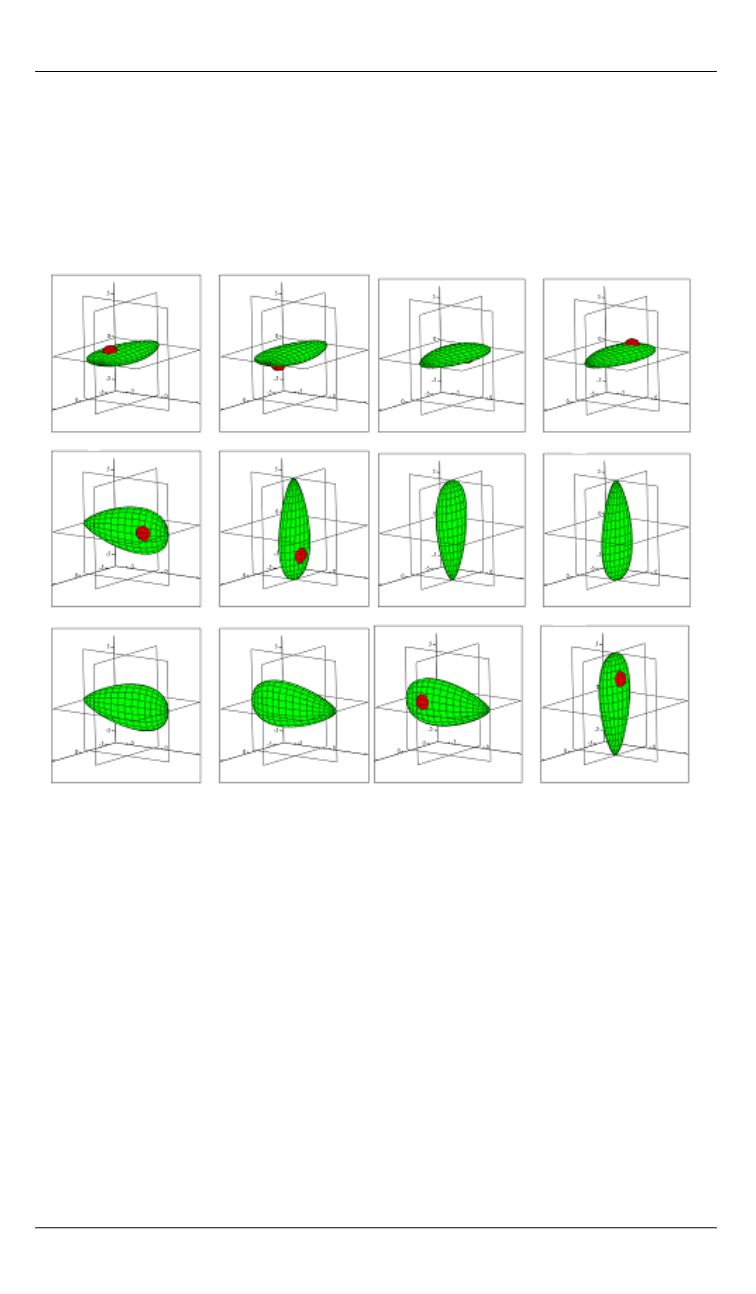
мерно заполняющих все ориентационное пространство (рисунок).
12 ориентаций твердого тела, равномерно заполняющих
ориентационное пространство
Заключение.
Представленные результаты являются продолжени-
ем серии исследований авторов, посвященной математическому мо-
делированию равномерных распределений точек на поверхностях
и их применению в различных исследованиях. Полученные ранее ре-
зультаты по моделированию случайных распределений на гиперпо-
верхностях и, в частности, на трехмерной гиперсфере, основанные на
описании непрерывного равномерного распределения, в совокупно-
сти с использованием центросимметричных правильных простран-
ственных многогранников позволили получить метод для равномер-
ного дискретного заполнения ориентационного пространства.
Результаты, представленные в данной статье, могут быть полезны
для ряда теоретических научных направлений, а также в практиче-
ских приложениях. К примеру, моделирование случайных ориента-
















