
Стабилизация ориентации спутника с помощью двух спарок гиродинов
Инженерный журнал: наука и инновации
# 7·2017 9
2
2
1
( )
sup
( , )
( , ).
m
u
u
c
c
y
y
c
α β
α β
y
Будем искать
1 2
2
2
2
1
4
1
1
min
min ( , )
( , )
i
i
u
c
c
α β
α β
не только по мнимым
1 2
,
,
но и по действительным
1 2
,
частям
корней характеристического уравнения системы. Минимум
2
u
ищем в замкнутой области D:
1
1,
2
1,
1
500
500,
2
500
500,
методом сопряженных градиентов, начиная спуск с
точки
1
1,
2
1,
1
10,
2
10.
Получаем
2
D
min
6,18459
u
при
1
1,
2
1,
1
1 , 205,
2
0, 00012.
Подставляем найденные
1 2
, ,
1 2
,
в формулу управления:
2
1
2
3
(0)
(0)
1
2
1
2
0, 4316 1, 64354 0, 425326
0, 5309
1,81649
.
u
s r
s r
Поведение системы (5), (7) под действием построенных управлений
при начальных условиях
1
(0) 0,16,
2
(0)
0, 02,
3
(0)
0, 04,
1
(0)
0, 7768,
q
2
(0)
0, 339,
q
совпадающих с конечными значе-
ниями переменных, полученными в предыдущем разделе, показано
на рис. 3 и 4. При этом решается задача ориентации спутника в
направлении орта
0
0.(3), 0.(6), 0.(6) .
r
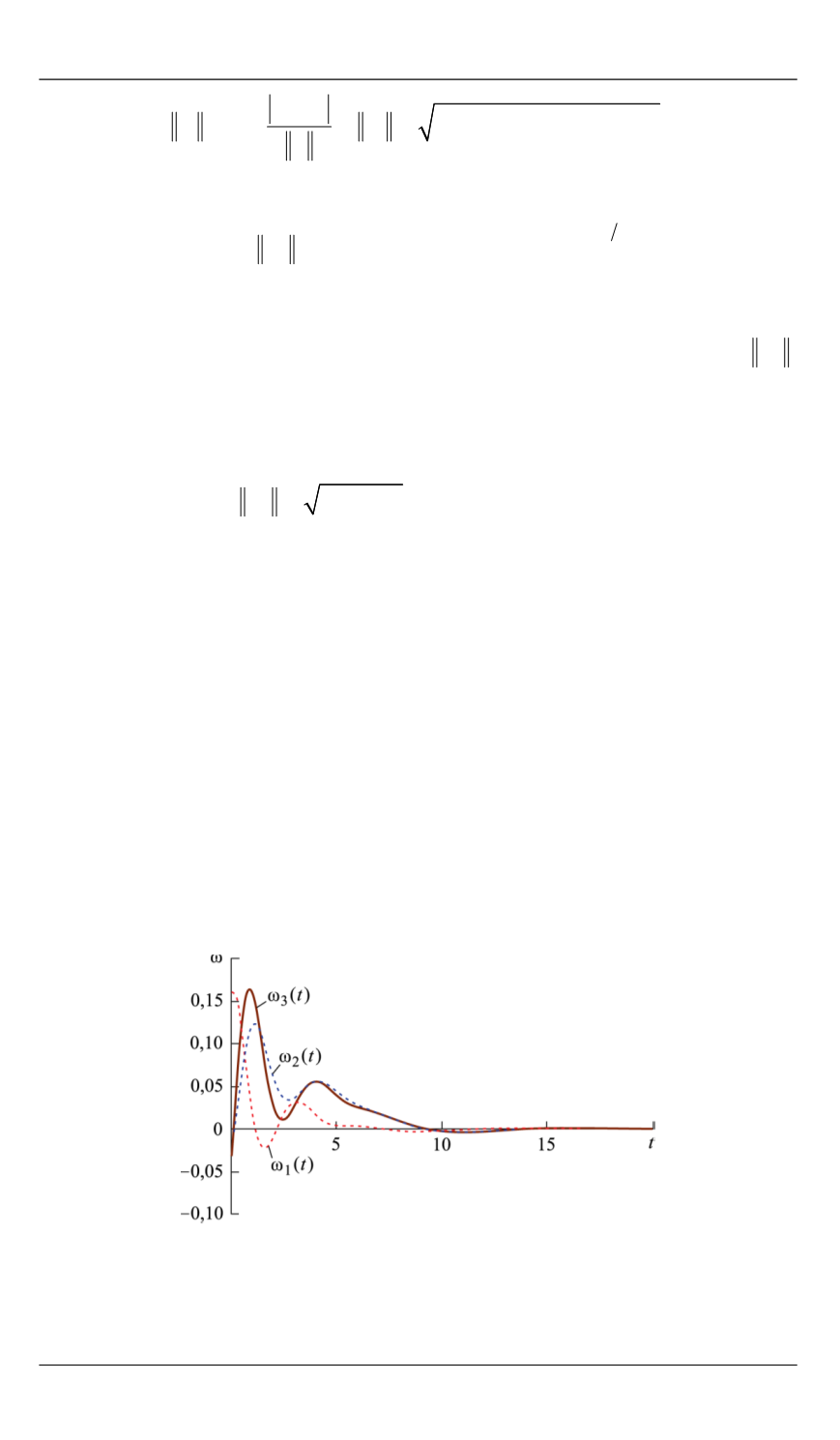
Рис. 3.
Проекции угловой скорости:
5
1
(20) ( 5) 10 ;
5
2
(20) ( 9) 10 ;
5
3
(20) ( 9) 10
















