
Выбор оптимального аккумулятора для многороторного беспилотного вертолета…
Инженерный журнал: наука и инновации
# 5·2017 7
Используем такой же критерий и в рассматриваемом случае. Как
и в работе [3], рассмотрим относительное время полета, т. е. время,
отнесенное к максимально возможному времени полета. Уравнение
для определения относительной массы
инт
m
по интегральному крите-
рию можно записать так:
max
.
m
τ =
τ
(16)
Значение
max
τ
можно найти подстановкой в формулу (5) значе-
ния
опт
,
m
которое определяется по формуле (14). Условимся, что в
дальнейших выкладках опустим коэффициент
K
, который не влияет на
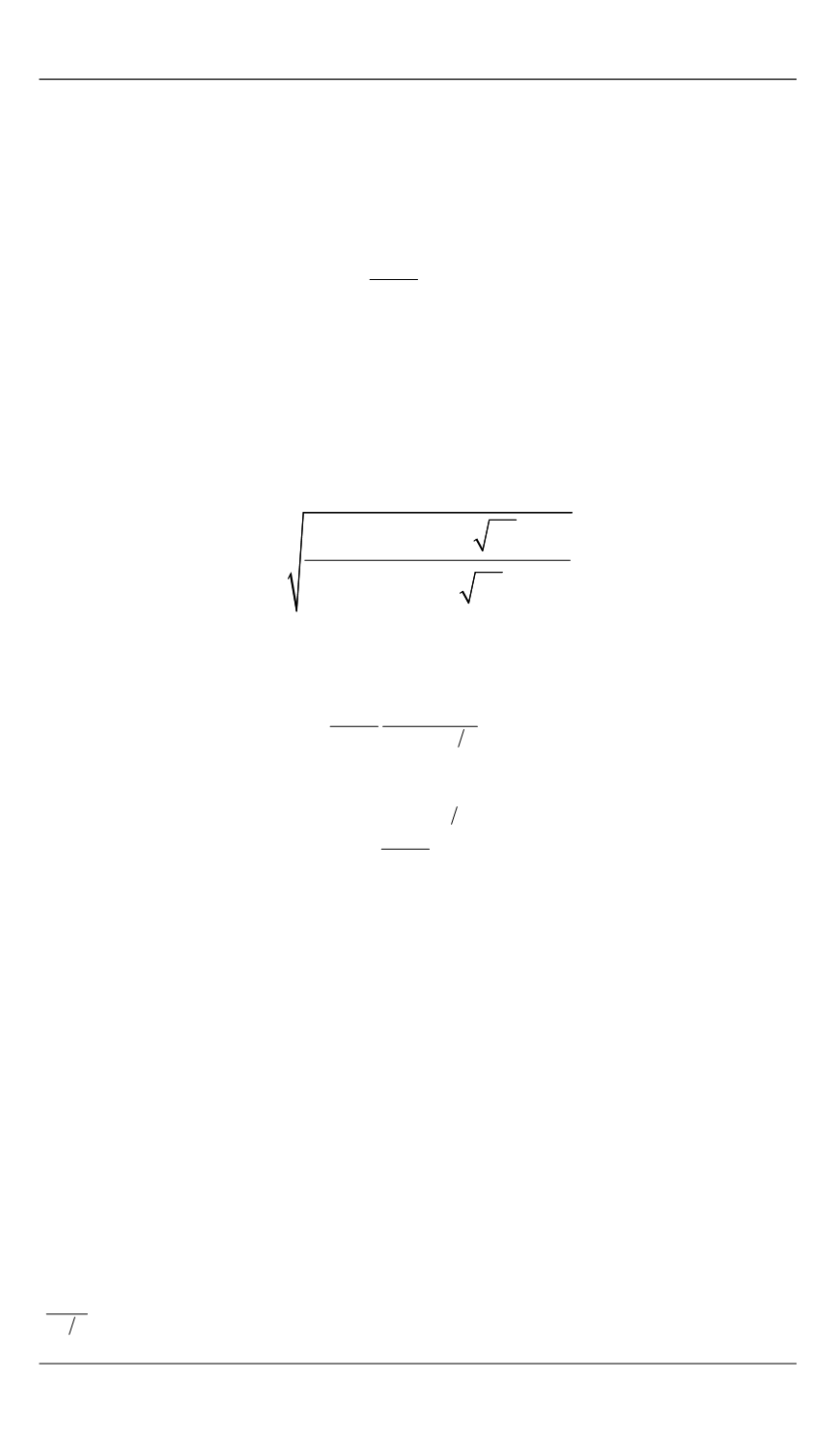
относительное время полета. После подстановок и преобразований по-
лучаем
(
)
(
)
100
100
max
100
3
100
100
2 1
2
4 1
3
T
T
T
k
k
k
− η + η
τ = η
− η + η
. (17)
Уравнение (16) с учетом формулы (5), если опустить
K
,
запишем
как
вис
3 2
max
,
(1 )
М
m m
m
η
=
τ
(
(18)
а его решение будет следующим:
2 3
вис
инт
max
1,
M
m
η=
−
τ
(19)
где
вис
M
η
вычисляется по формуле (2), а
max
τ
— по формуле (17).
Следует отметить, что использование выражения (5) в приведен-
ных для получения формулы (19) выкладках не означает, что зависи-
мость времени полета от массы аккумулятора в рассматриваемом
случае такая же, как и в модели, не учитывающей изменение КПД
мотора. Зависимость (5) при фиксированных η
100
и
k
T
показывает, как
будет изменяться время полета, если при каждом значении
m
обеспе-
чивается заданная фиксированная тяговооруженность (значение
k
T
).
Это предполагает, что масса ЛА без аккумулятора не остается посто-
янной. Зависимость времени от
m
при фиксированной массе
M
0
вы-
ражается формулой (9). Именно максимум этой функции использует-
ся для нормирования времени в уравнении (16).
Значение
инт
m
при изменении η
100
от 1 до 0 составляет от
2 3
3 1 0,89
2
− ≈
до 1. При значениях η
100
и
k
T
, соответствующих пара-
















