
Выбор оптимального аккумулятора для многороторного беспилотного вертолета…
Инженерный журнал: наука и инновации
# 5·2017 5
(
)
(
)
100
100
опт
100
100
2 1
.
2 1
T
T
k
m
k
− η + η
=
− η + η
(14)
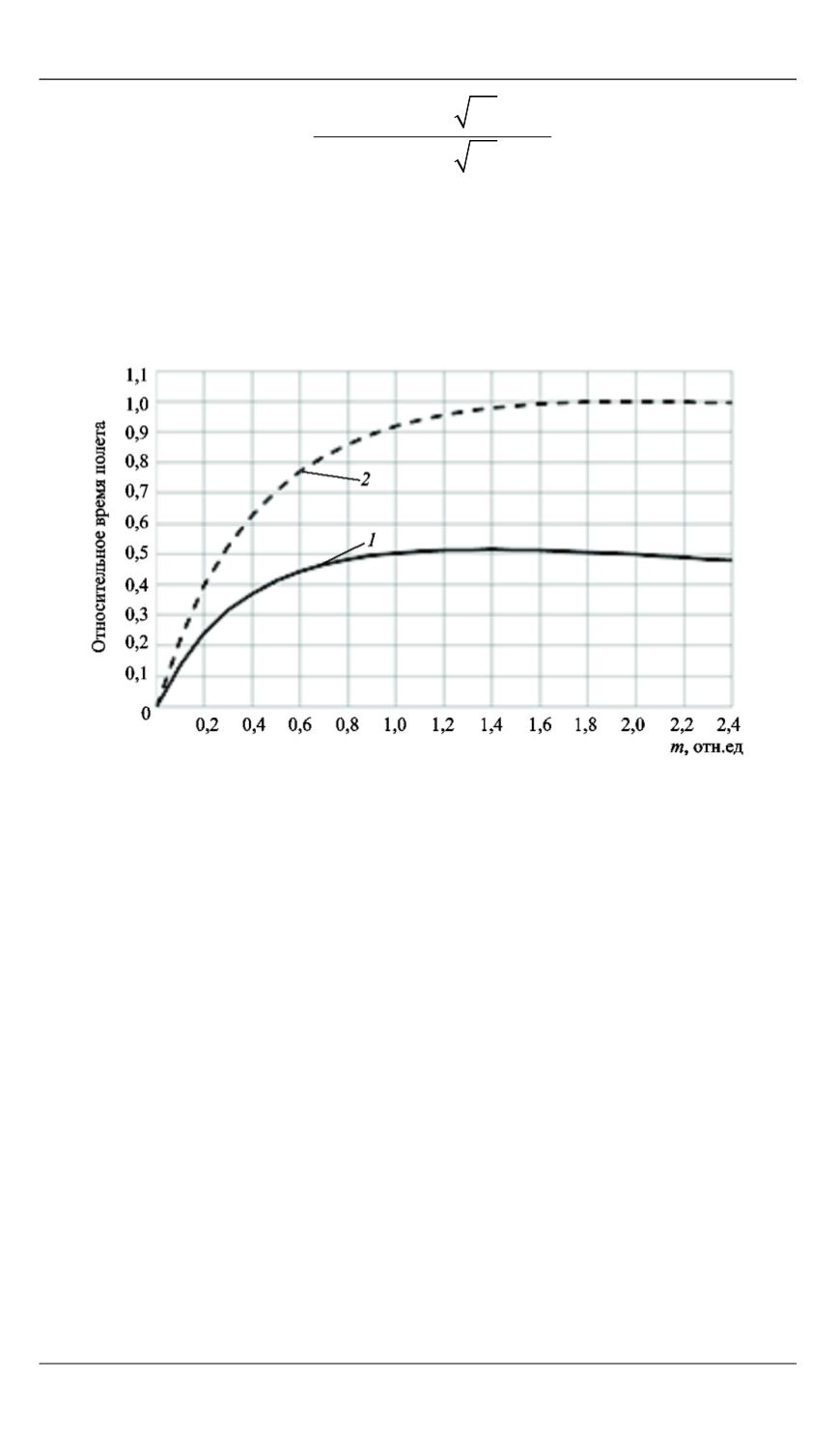
Графики зависимости времени висения от относительной массы
аккумуляторной батареи построены в соответствии с формулой (9)
(рис. 3). Значения по оси ординат нормированы так, чтобы макси-
мальное значение в варианте
2
было равно 1.
Рис. 3.
Зависимость относительного времени полета от относительной
массы аккумуляторной батареи:
1
— η
100
= 0,65,
k
T
= 1,7,
k
T
0
= 4,33;
m
опт
= 1,55;
2
— η
100
= 1,
m
опт
= 2,0
Рассмотрим частные случаи. Если η
100
= 1, что соответствует мо-
тору с идеально жесткой характеристикой и КПД = 100 %, по форму-
ле (14) получаем
опт
m
= 2 (кривая
2
, рис. 3). Это значение совпадает с
найденным в работе [3] для модели, в которой КПД мотора считается
постоянным при изменении массы аккумулятора. При η
100
, стремя-
щемся к нулю, формула (14) дает
опт
m
= 1. При 0 < η
100
< 1 значение
относительной массы аккумуляторной батареи, при котором достига-
ется наибольшее время висения, находится в пределах от 1 до 2, за-
висит от тяговооруженности и монотонно возрастает с ростом η
100
.
На рис. 4 приведена зависимость оптимального значения относи-
тельной массы аккумуляторной батареи от η
100
при двух значениях
тяговооруженности
k
T
. При тяговооруженности, равной 4, что мож-
но считать верхним пределом для реальных ЛА, зависимость линей-
на;
k
T
= 1 — это теоретический нижний предел тяговооруженности.
















