
Ю.В. Захарова, Л.Г. Лохматова
2
Инженерный журнал: наука и инновации
# 11·2016
В настоящее время для решения задач о напряженно-дефор-
мируемом состоянии (НДС) изделия используется метод конечных
элементов (МКЭ) [11–16]. В данной работе с помощью МКЭ решена
задача моделирования НДС цилиндрической оболочки из
композиционного материала с дефектами, рассматриваемой в рамках
теории Тимошенко [17, 18], под действием равномерного внутреннего
давления.
Математическая постановка задачи моделирования НДС
композиционной оболочки с дефектами.
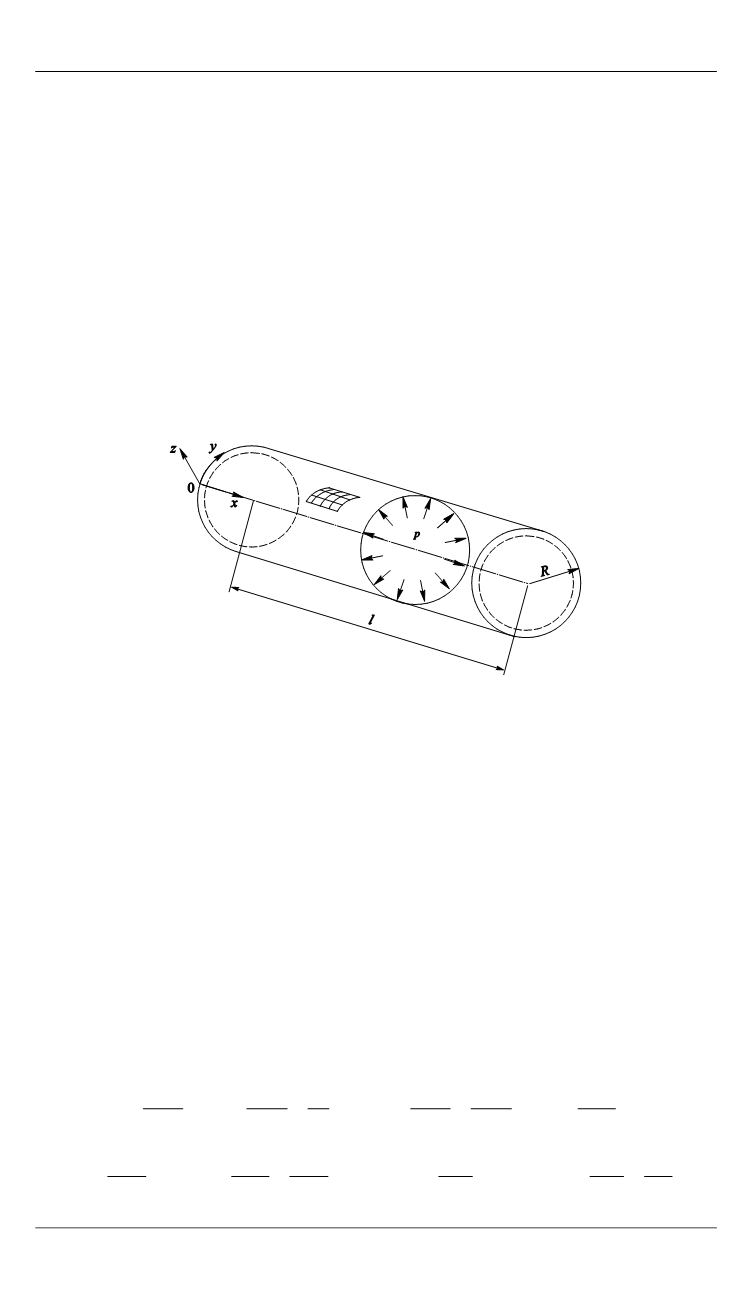
Рассмотрим цилиндри-
ческую оболочку из композиционного материала, находящегося под
действием равномерного внутреннего давления
р
(рис. 1). В качестве
кинематической гипотезы примем гипотезу Тимошенко для
многослойного пакета [18, 19].
Рис. 1.
Геометрия цилиндрической оболочки
В качестве координатной поверхности (
z
= 0) примем среднюю
поверхность оболочки. Тогда распределение по толщине оболочки
будем вычислять по формулам
,
, ,
,
u U z
x y w W
α α α
= + ϑ α =
=
(1)
где
,
x
U
y
U
— тангенциальные перемещения;
W
— прогибы оболоч-
ки;
,
x y
ϑ ϑ
— углы поворота сечений.
С учетом принятой гипотезы и геометрии рассматриваемой
оболочки деформационные соотношения примут вид
,
,
,
x
x
x
y
y
y
xy
xy
xy
е z
е z
e z
ε = + χ ε = + χ ε = + χ
(2)
где
;
; 2
;
;
; 2
;
;
.
y
y
x
x
x
x
y
xy
x
y
y
y
x
y
xy
x
xz
y
yz
U
U
U
W
U
е
е
е
x
y r
y
x
x
U
W
W
y
y
x
x
x R
∂
∂
∂
∂
∂ϑ
=
= +
= +
χ =
∂
∂
∂ ∂
∂
∂ϑ
∂ϑ ∂ϑ
∂
∂
χ =
χ = +
ϑ = γ −
ϑ = γ − +
∂
∂ ∂
∂
∂
(3)
















