
Ю.В. Захарова, Л.Г. Лохматова
8
Инженерный журнал: наука и инновации
# 11·2016
Также был проведен расчет напряжений по безмоментной теории
для оболочки с исходными параметрами, но не имеющей закрепле-
ний на торцах, в соответствии с работами [17, 18, 22]:
7
6, 7 10
yy
pR
h
p = = ⋅
Па.
При численном решении данной задачи получены результаты,
представленные на рис. 6.
Рис. 6.
Распределение окружных
напряжений в оболочке со сво-
бодными концами
В соответствии с представленными на рис. 5 и 6 данными в обоих
случаях результаты численных решений довольно близки по значе-
ниям к результатам, полученным при аналитических решениях. От-
носительная погрешность не превышает 7 %. Это доказывает, что
разработанная модель и алгоритм работают верно.
Также проведено параметрическое исследование зависимости
НДС оболочки от размера, физико-механических свойств дефекта и
его расположения в оболочке.
На рис. 7–10 представлены результаты численного моделирова-
ния НДС цилиндрической оболочки с дефектами.
Исходя из данных рис. 7–10 можно сделать вывод, что при оди-
наковых параметрах дефекта материал деформируется сильнее, если
дефект примыкает к торцу оболочки.
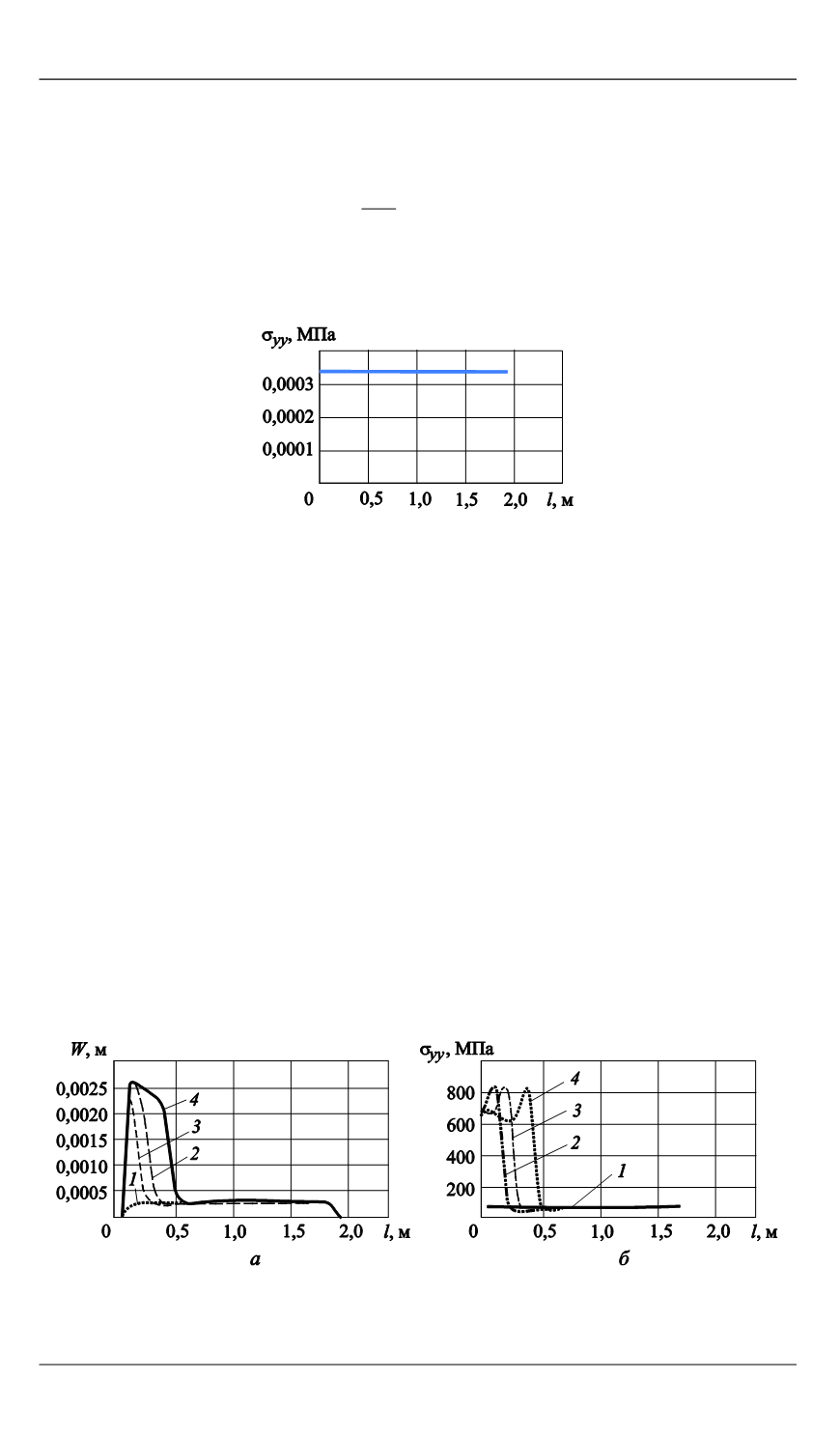
Рис. 7.
Зависимость прогибов (
а
) и окружных напряжений (
б
) от размера дефекта,
примыкающего к торцу оболочки:
1
— без дефекта;
2
–
4
— S
об
/S
деф
равно 784, 392 и 31 соответственно
















