
Н.В. Котюженко, Л.А. Савин
8
Инженерный журнал: наука и инновации
# 2
2016
Матрицы однородного преобразования координат звеньев
манипуляторов.
После построения DH-координат для всех звеньев
манипулятора можно построить упомянутые ранее однородные мат-
рицы преобразования, имеющие размерность 4×4 и связывающие
i
-ю
и (
i
– 1)-ю системы координат [2, 3]. Построение матриц преобразо-
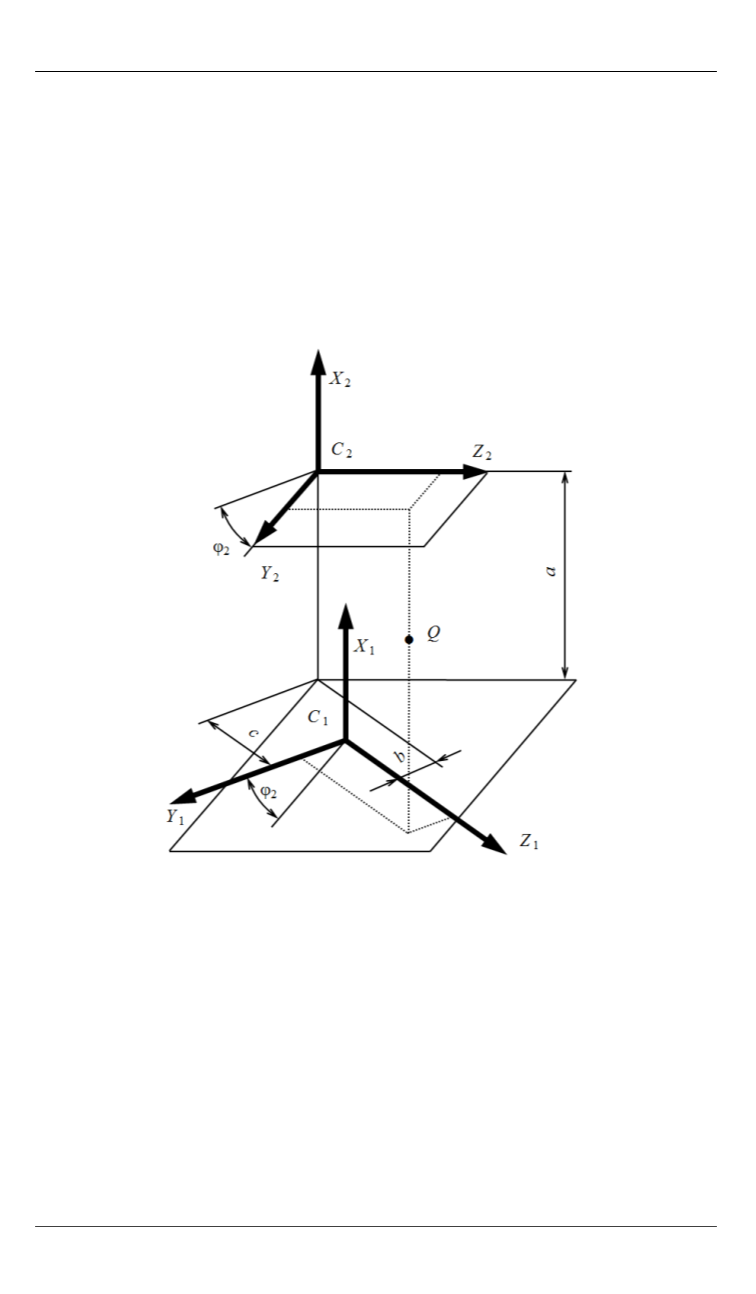
вания можно продемонстрировать на следующем примере. На рис. 5
изображены две системы координат
C
1
и
C
2
. При этом система
C
2
от-
личается от системы
C
1
поворотом вокруг оси
X
2
на угол φ
2
и смеще-
нием начала координат на величину отрезков
a
,
b
и
c
. Рассмотрим пе-
реход от системы
C
2
к системе
C
1
с помощью матриц.
Рис. 5.
Пример перехода от системы координат
C
2
к
C
1
В однородных координатах положение некоторой точки
Q
в соот-
ветствующих системах запишется в виде
Q
(
X
1
,
Y
1
,
Z
1
,
t
1
) и
Q
(
X
2
,
Y
2
,
Z
2
,
t
2
).
Однородными координатами
точки в трехмерном пространстве
называются любые четыре числа
X
1
,
Y
1
,
Z
1
,
t
, связанные с ее декарто-
выми координатами (
X
,
Y
,
Z
) равенствами
X
=
X
1
/
t
;
Y
=
Y
1
/
t
;
Z
=
Z
1
/
t
,
где
t
— коэффициент масштабирования.
Коэффициенты масштабирования примем равными единице:
t
1
=
t
2
= 1. Такое масштабирование соответствует принятым допуще-
ниям о неизменности геометрических размеров между осями шарни-
















