
Ю.В. Баркин, М.Ю. Баркин
6
2
2
2
1
2 ;
m
m
m m m
n b c a
2
2
2
1
2 ;
m
m
m m m
n c a b
2
2
2
2 .
m
m
m m m
n a b c
Уравнения (11) допускают тривиальное решение
0,
x y z
для которого центр масс ядра совпадает с центром масс оболочки. В
общем случае эти уравнения легко интегрируются (при произволь-
ных начальных условиях
0
0
0
,
,
x x y y z z
) и описывают соответ-
ствующие движения внутреннего ядра [3, 5].
Колебательные движения твердого ядра имеют место при усло-
вии, что все корни характеристического уравнения системы (11) яв-
ляются чисто мнимыми. При этом три вещественные частоты коле-
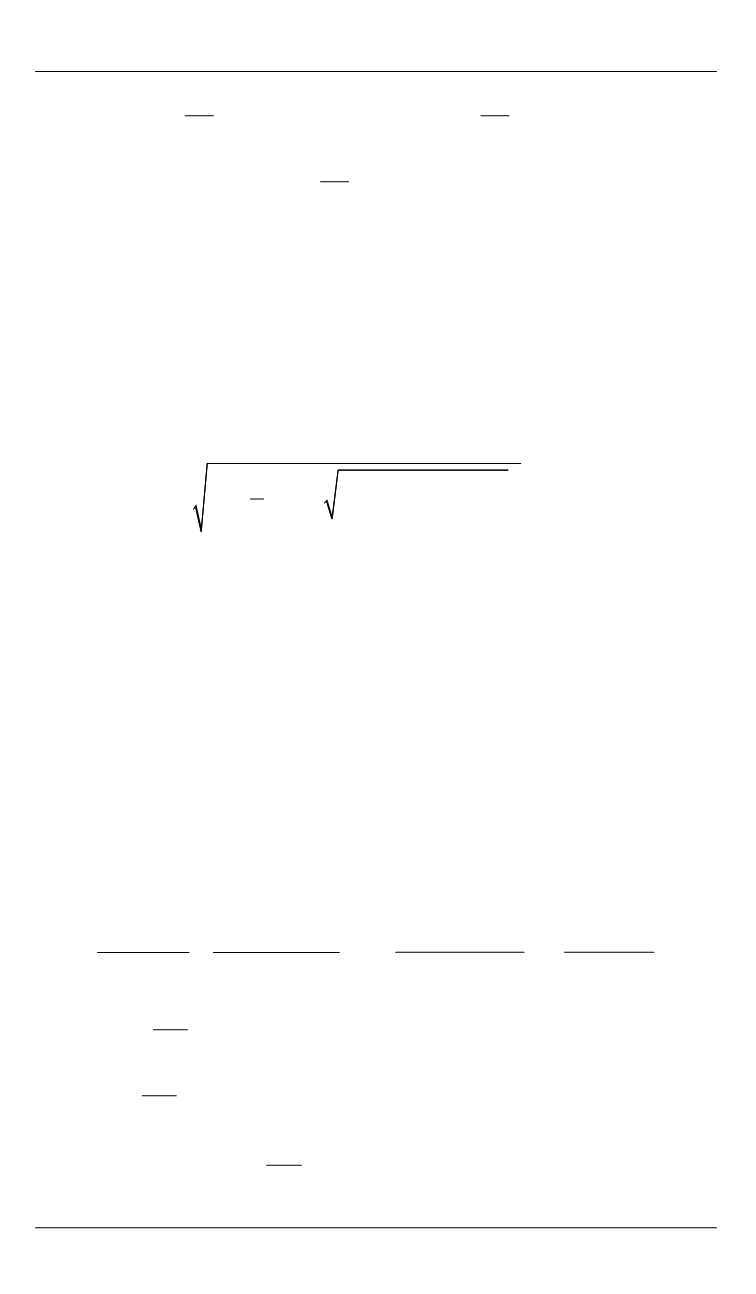
баний определяются формулами
2
2
2
2 2
1,2
1 1
2
4
;
2
m
m
m m
3
m
.
Таким образом, условия устойчивости внутреннего ядра записы-
ваются в виде
2
0,
m
2 2
2 2
2
4
0.
m
m m
Эти условия выполняются в случае сжатой вдоль оси
m
C z
эллипсои-
дальной оболочки.
Вращение тела
i
P
не зависит от его орбитального движения и опи-
сывается независимыми дифференциальными уравнениями (9), (10).
Уравнения вращательного движения ядра в канонических
переменных Эйлера и Андуайе.
Введем по известным правилам [6]
канонические импульсы
,
p p
и
,
p
сопряженные углам Эйлера
, , ,
и опишем вращательное движение ядра вместо уравнений
(9), (10) каноническими уравнениями:
, ,
, ,
d
F
dt
p p p
;
, ,
, ,
d p p p
F
dt
; (12)
2
2
1 cosec
cos sin
sin cos
2
i
F
p p
p
A
2
2
1 cosec
cos cos
sin sin
2
i
p p
p
B
2
1
, ,
2
i
p p U
C
, (13)
















