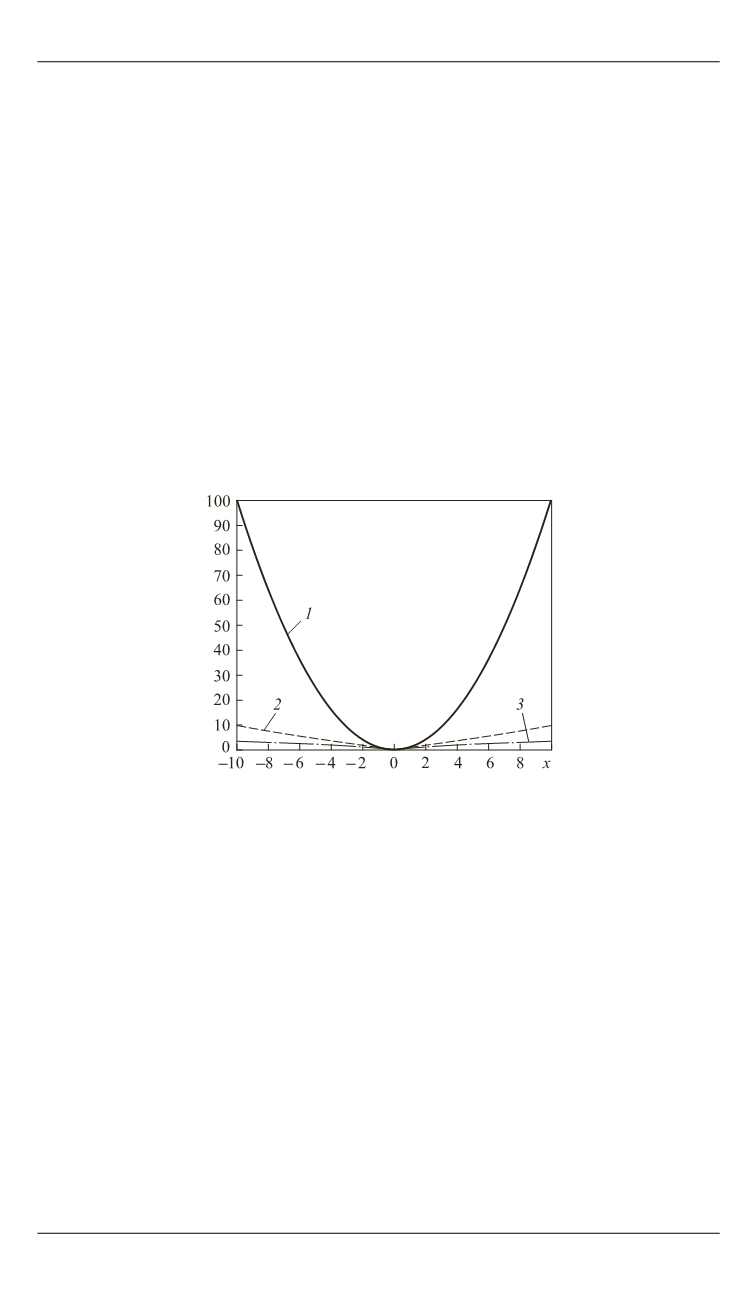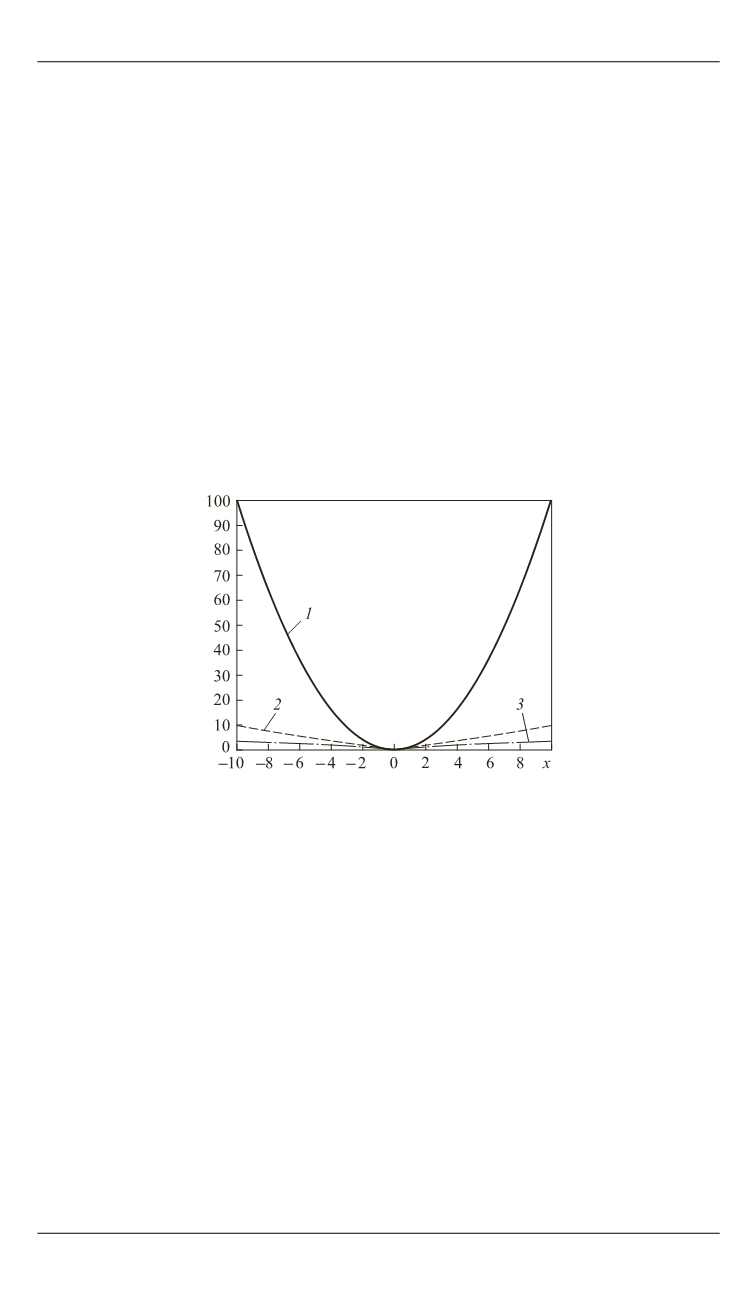
А.А. Грешилов
6
амплитуд (мощностей) по пеленгам (угловой спектр). В идеальном
случае (шумы отсутствуют) количество ненулевых элементов векто-
ра
u
равно количеству фактически присутствующих в эфире ИРИ.
Положение ненулевых элементов в векторе
u
(в сетке пеленгов) ха-
рактеризует пеленги соответствующих ИРИ. Таким образом, введе-
ние сетки пеленгов решает не только проблему нелинейности задачи,
но и проблему определения количества ИРИ. Количество узлов сетки
намного больше количества ИРИ, т. е. большинство элементов век-
тора
u
в идеальном случае равны нулю. Несмотря на линейность, за-
дача (6) остается некорректной.
Решив систему линейных алгебраических уравнений (6), получа-
ем оценки искомых величин.
Для того чтобы решить подобные задачи, применяют методы ре-
гуляризации [1], в которых дополнительно вводят стабилизаторы,
определяющие форму решения.
Рис. 2.
Зависимость штрафа различных стабилизаторов от показателя
степени
р
= 2 (
1
),
р
= 1 (
2
) и
р
= 0,5 (
3
)
Графики зависимости штрафов различных стабилизаторов от
р
представлены на рис. 2, на котором видно, что стабилизатор Тихоно-
ва (
р
= 2) накладывает намного больший штраф на мощные состав-
ляющие вектора решения, чем другие стабилизаторы. Этим объясня-
ется «сглаженность» решений, получаемых методом Тихонова.
Наименьший штраф на мощные составляющие решения накладыва-
ют
1
l
- (
р
= 1) и
0,5
l
-стабилизаторы (
р
= 0,5). Таким образом,
p
l
-
стабилизаторы при
0
1
p
являются более подходящими для реше-
ния задач, в которых большинство элементов вектора решения равны
нулю. Однако недостатки этого функционала уже указаны.