А.А. Грешилов
12
4.
Данные поступают в блок определения точки минимума
функционала (10) с заданным шагом обновления направления спуска.
Затем по аналитическим формулам находят значения пеленгов всех
сигналов, поступивших на АС.
5.
Пеленги поступают на блок вычисления дисперсий оценок пе-
ленгов.
6.
Вывод углового спектра (пеленгационной панорамы).
Приведенные процедуры не содержат ни параметров регуляриза-
ции, ни дополнительных сглаживающих операторов. Регуляризация
решения обеспечивается формой (видом) функционала (10). Проце-
дуры используют простейшие математические операции, благодаря
чему обеспечивается малое время вычислительного процесса.
Алгоритм в работе [1] исследован на функциях, имеющих участ-
ки с резким изменением значений производных (рис. 3). Идеальная
ступенчатая функция свертывалась с ядром (линия
3
на рис. 3). Затем
по описанному алгоритму определения точки минимума функциона-
ла (10) восстанавливалась исходная функция. Ступенчатая функ-
ция — более сложная функция, чем пеленгационная панорама.
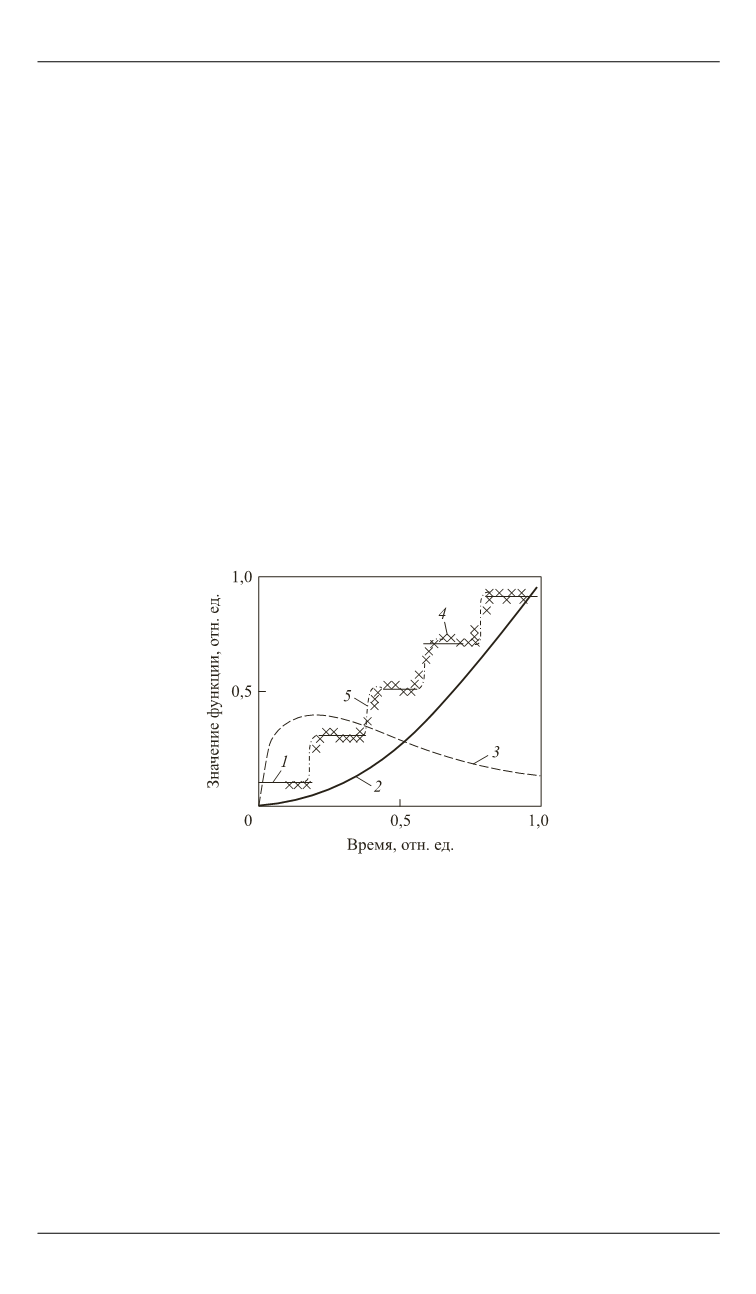
Рис. 3.
Восстановление ступенчатой функции:
1
— заданная ступенчатая функция;
2
— результат свертки с ядром;
3
— ядро;
4
,
5
— результаты восстановления соответственно
после 100 и 300 итераций
Результаты восстановления ступенчатой функции методом со-
пряженных градиентов при различном числе итераций приведены на
рис. 3. Начальные приближения принимали постоянными и равными
1. На рис. 3 видно, что с увеличением числа итераций (до 300) полу-
чаемые приближения искомой функции монотонно стремятся к точ-
ному значению.
Пример
.
Приведем результаты модельного расчета пеленга на
компьютере с тактовой частотой процессора 2 ГГц.


