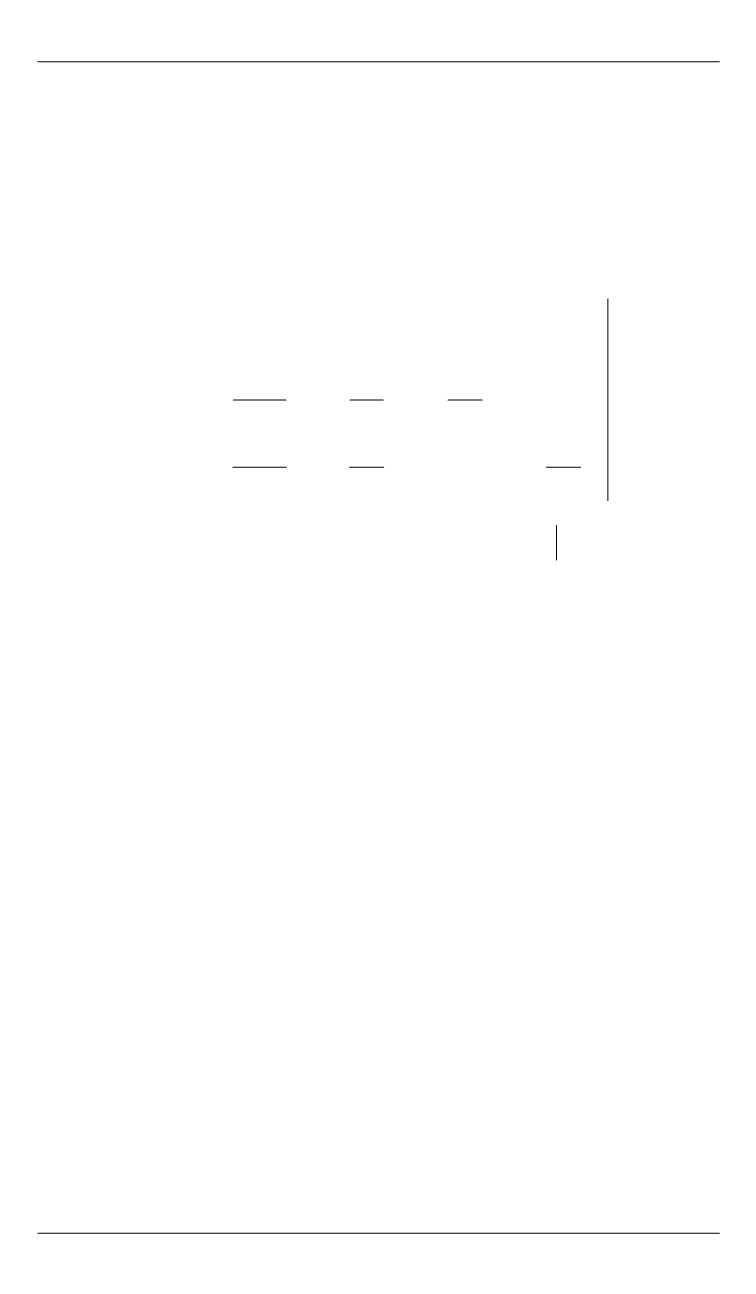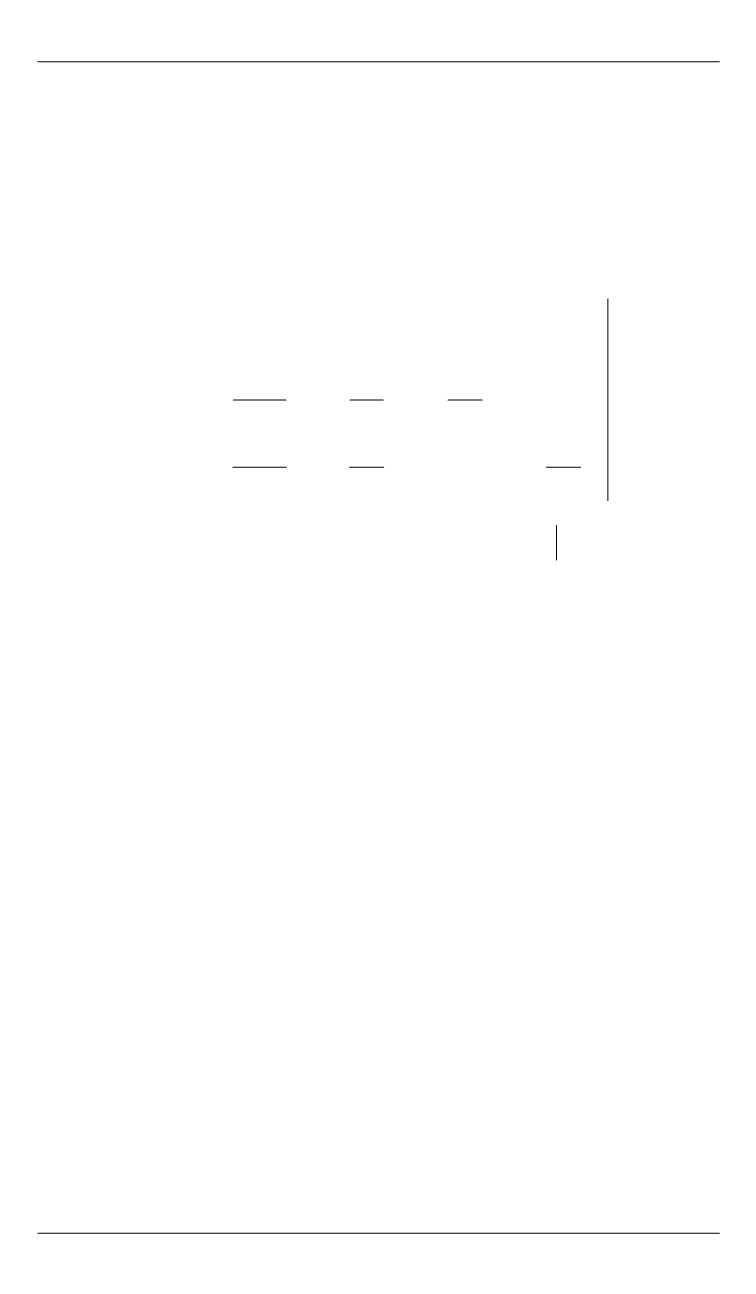
Н.Е. Зубов, Е.А. Микрин, А.С. Олейник
4
0 0 2
0 2
T
0
1 3
4
[0 2 {( ) ( ) } 0 0]
F
x x
x
= −
+
.
(2.4)
В дискретном случае система (2.2) будет иметь следующий вид:
Д
( 1)
( ) ( )
( )
x n
A n x n F n
+ =
+
,
(2.5)
где индекс
n
— номер такта работы дискретной системы,
h
= 0,2 с —
период квантования (длительность такта вычислительной бортовой
ЭВМ),
2 2
3 4
3 1
4 1
Д
3 2
3
2
2
1
1
1
4 2
4
2
2
1
1
1
1
0
0
(
)
1
2
2
2
2
2
( )
1
2
2
2
1
x
x
n
h
h x x
hx x
hx x
x x
x
x
A n
h
h
h
h
x
x
x
x x
x
x
h
h
h
h
x
x
x
⎡
⎤
⎢
⎥
+ ⎢
⎥
⎢
⎥
=
−
−
Ω
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
−
−Ω −
⎢
⎥
⎣
⎦
,
(2.6)
2
2
1
3
4
( ) [0 2 {( ) ( ) } 0 0]
T
n
F n
x h x
x
= −
+
.
(2.7)
3. Алгоритм точного размещения полюсов при решении задач
наблюдения и идентификации.
Далее будем рассматривать дина-
мический объект, описываемый уравнениями вида
( 1)
( ) ( ) ( )
x n
A n x n F n
+ =
+
,
( )
( )
y n Cx n
=
.
(3.1)
Наблюдатель полного ранга для системы (3.1) определяется
уравнением
ˆ
ˆ
ˆ
ˆ
( 1) ( ( )
) ( )
( )
( )
x n
A n LC x n Ly n F n
+ = −
+ +
.
(3.2)
Объединив (3.1) и (3.2), получим уравнение невязок
( 1) ( ( )
) ( )
L
x n
A n LC x n
+ =
−
.
(3.3)
В соответствии со сформулированной задачей известными пара-
метрами измерения являются
x
1
,
x
2
и неизвестными —
x
3
,
x
4
. Следо-
вательно, матрица
С
имеет вид
1 0 0 0
.
0 0 0 0
C
⎛
⎞
= ⎜
⎟
⎝
⎠
Для получения матрицы
A
L
для системы (2.5) необходимо разло-
жить
x
(
n
+ 1) и
F
(
n
) в ряд Тейлора в окрестности точки
x̂
(
n
):
2
2
3 1
3 1 3
4 1
4 1 4
ˆ
ˆ
ˆ
ˆ
ˆ
( 1)
( 1) (2
4 )
(2
4 ) ,
x n
x n
hx x hx x x hx x hx x x
+ = + +
+
+
+
(3.4)