Н.Е. Зубов, Е.А. Микрин, А.С. Олейник
10
1
1
1
ˆ
( )
( )
( )
n x n x n
ε = −
,
2
2
2
ˆ
( )
( )
( )
n x n x n
ε = −
.
(4.12)
Рассмотрим несколько численных примеров оценки угловой ско-
рости линии визирования по результатам измерения дальности и ско-
рости продольного движения для различных наборов начальных зна-
чений вектора состояния активного КА относительно пассивного.
Величина
2
2
ˆ
ˆ
y
z
Ω + Ω
представлена на конец пятой вычислительной
итерации. Результаты сведем в таблицу.
№
D
, м
Ḋ
, м/с
,
1/ с
y
Ω
,
1/ с
z
Ω
ˆ ,
1/ с
y
Ω
ˆ ,
1/ с
z
Ω
2
2
5
2
;
10 , 1 / с
y
z
−
Ω + Ω
2
2
5
2
ˆ
ˆ ,
10 1 / с
y
z
−
Ω + Ω
1. 200
–1,0
0,006
0,008 0,005 0,005 10,040
9,974
2. 150
–0,7 –0,003
0,007 0,005 0,005 5,821
5,794
3. 100
–0,5
0,003 –0,004 0,005 0,005 2,510
2,524
4. 50
–0,2 –0,009 –0,003 0,005 0,005 9,028
8,977
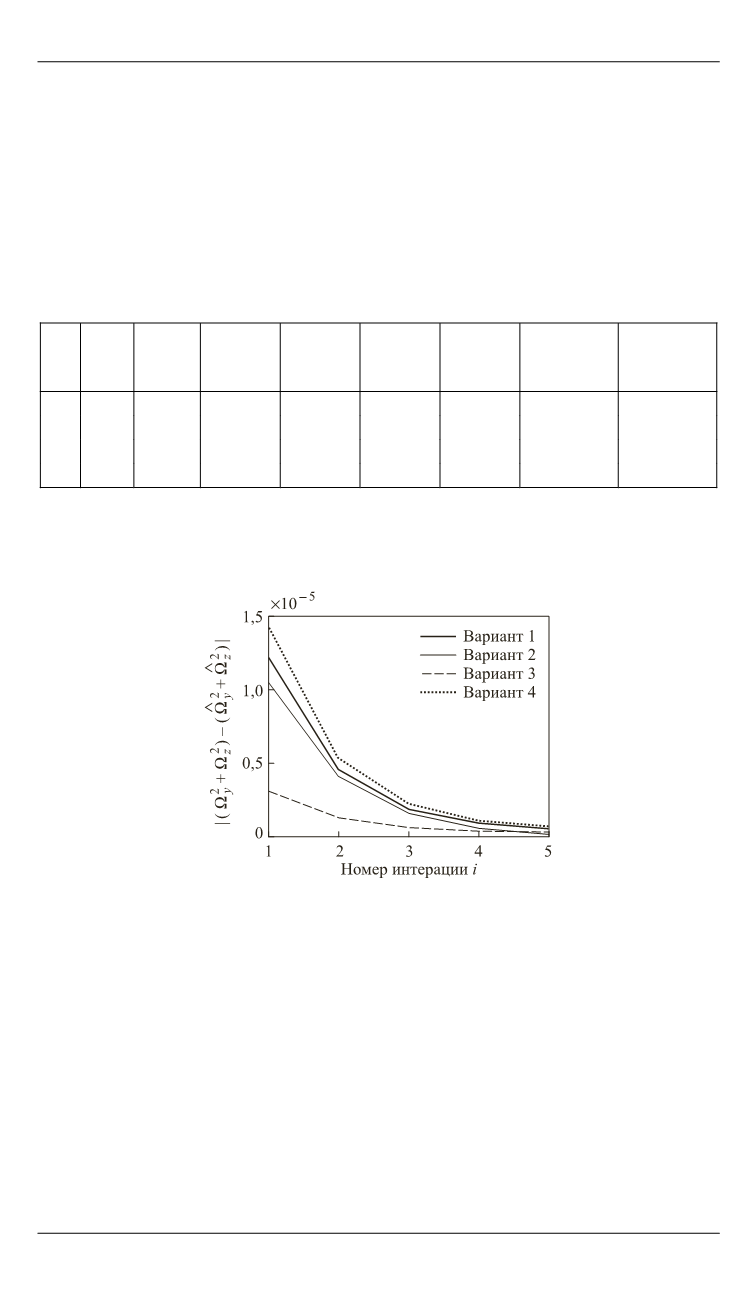
Изменение величины отклонения квадрата угловой скорости
линии визирования за пять вычислительных итераций представлено
на рис. 2.
Рис. 2.
Отклонение квадрата угловой скорости
линии визирования
Следовательно, за пять тактов работы бортового алгоритма обес-
печивается сходимость итерационного процесса оценки вектора уг-
ловой скорости линии визирования. Учитывая, что решение (4.9)
представляет собой аналитические выражения, вычислительные за-
траты незначительны, и он вполне может быть реализован в реаль-
ном масштабе времени.
Заключение.
В статье рассмотрена задача восстановления векто-
ра состояния при сближении космических аппаратов при наличии
отказа в канале измерения угловой скорости линии визирования. Раз-


