М.Ш. Мисриханов, В.Н. Рябченко, Н.Е. Зубов, Е.А. Микрин
6
Таким образом, задача
одновременной стабилизации
SIMO-
систем (1) и (2) сводится к задаче выбора вектора (28) во множестве
решений (26), (27).
Если указанный вектор выбран, то регулятор, одновременно ста-
билизирующий SIMO-системы (1) и (2), находится по формуле (16),
при этом полиномы и собственные значения матриц
(
)
T
( )
( )
1
i
i
i
i
i
A
−
− β − α
A b
T
(30)
являются устойчивыми.
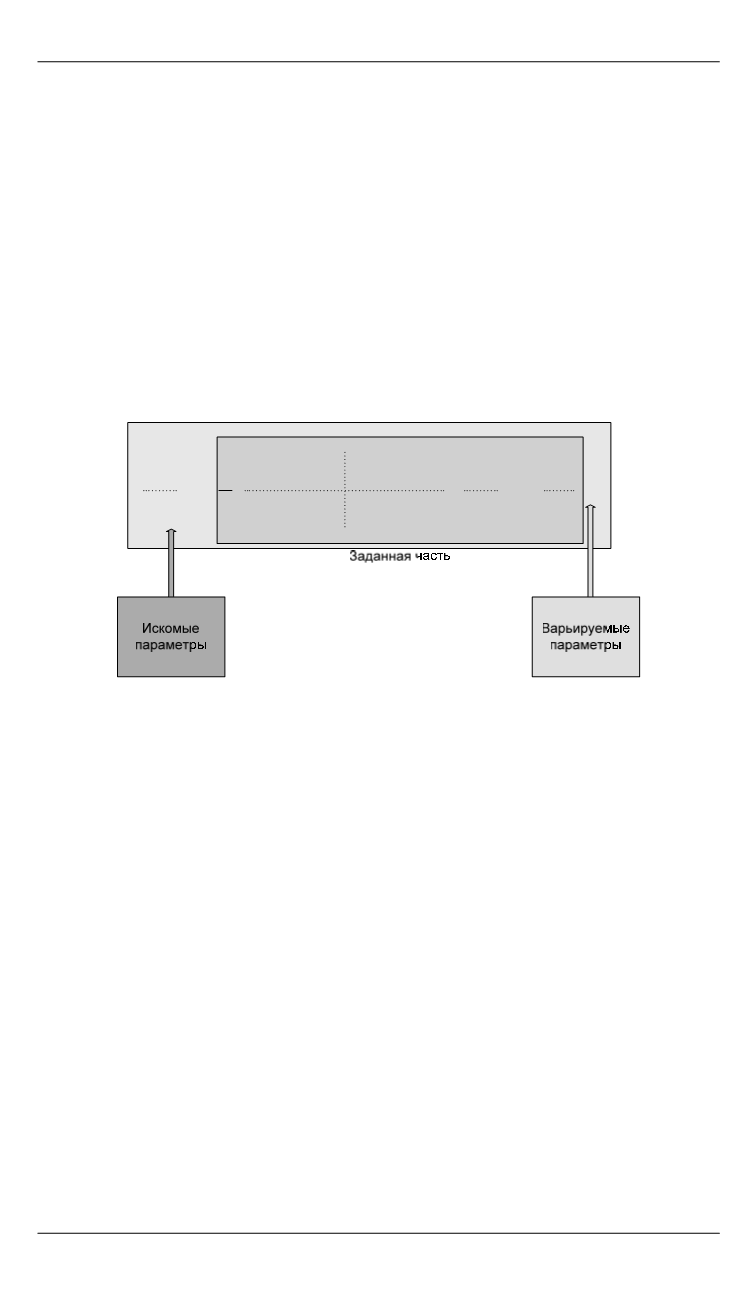
Схематично задача одновременной стабилизации двух систем
приведена на рис. 1.
T T
T
T T
T
1
2
1
2 1
2
(1)
(1)
(2)
(2)
1
2
n
A A
A
A A
n
A
β
α
ϕ
β
α
−
−
⎛
⎞
⎛ ⎞
⎛ ⎞
⎛ ⎞
− ⎟
⎟
⎟
⎟
⎜
⎜
⎜
⎜⎟
⎟
⎟
⎟
⎜
⎜
⎜
⎜
=
+ ⎟
⎟
⎟
⎟
⎜
⎜
⎜
⎜⎟
⎟
⎟
⎟
⎜
⎜
⎜
⎜
−
⎟
⎟
⎟
⎟
⎜
⎜
⎟
⎜
⎜
⎝ ⎠
⎝ ⎠
⎝
⎠
⎝ ⎠
T T
T
T T
T
I
I
Рис. 1.
Задача одновременной стабилизации двух систем
Из (26) вытекают
необходимые условия
одновременной стабили-
зации.
Лемма 1
.
Для одновременной стабилизации линейных SIMO-
систем
1
1 1
1 1
( )
( )
( )
t
t
u t
=
+
x A x b
,
2
2 2
2 2
( )
( )
( )
t
t
u t
=
+
x A x b
регулятором
n
∈
k
в законах управления
( )
( )
T
1
1
u t
t
= −
k x
,
( )
( )
T
2
2
u t
t
= −
k x
необходимо существование решения
φ
n
∈
линейного матричного
неравенства


