Н.А. Яскевич
8
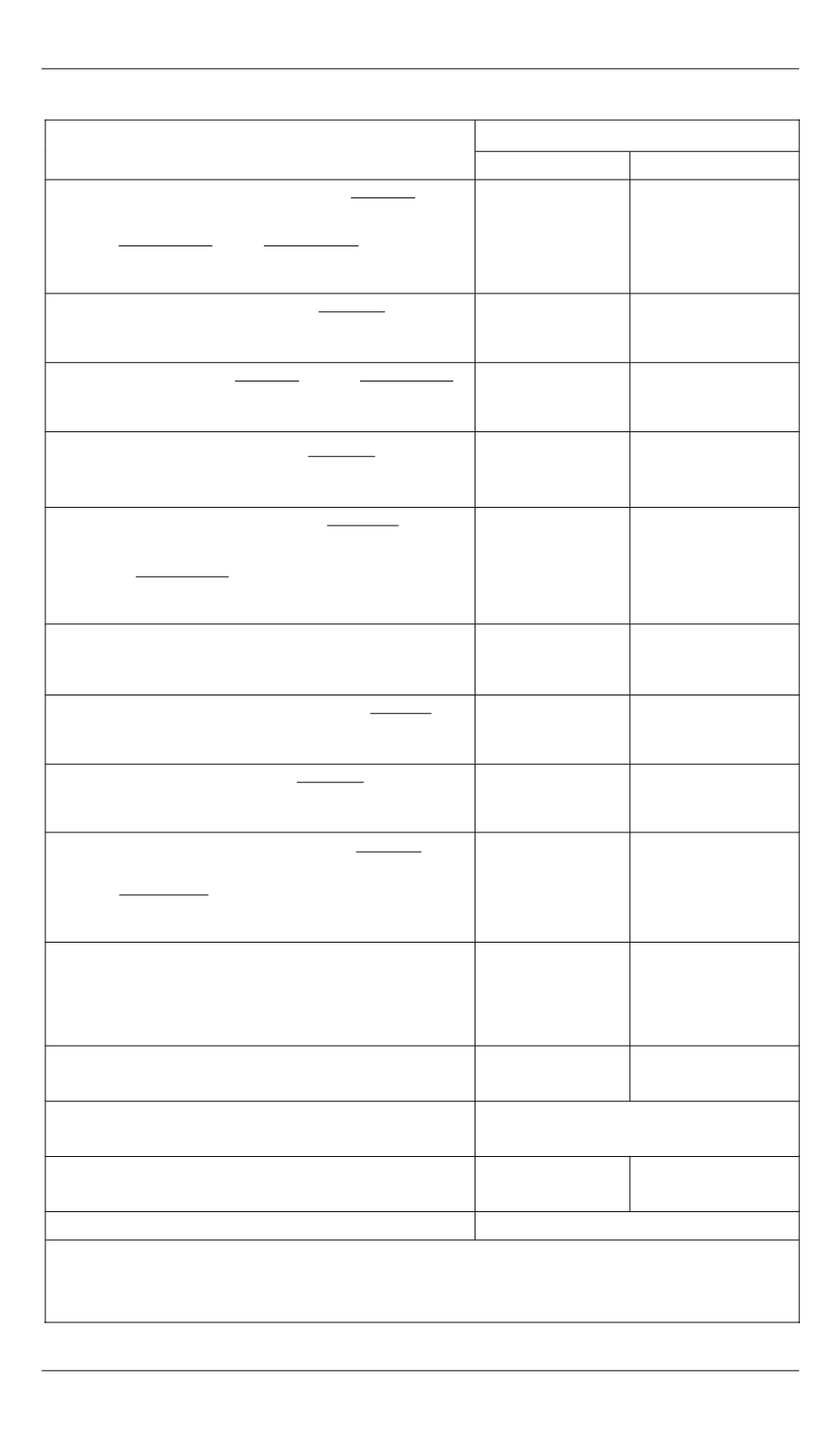
Окончание табл.
Вектор, матрица
Число
умножений
сложений
, 3
*
,3
, ,
,
,
, , 1
*
,
3,1 ,
2, 1,
1,
1
i j k
i k j k
i j k
i N
j N i
k N j
∑
Σ
+
=
+
= −
= − + = − +
I
c r
I
т
2
N
3
–12
N
2
+
+22
N
–12
2,5
N
3
–5
N
2
+
+27,5
N
–15
, 4
, 3
,
1
,
1,
,
2,1
i N
i N N
i N
∑
∑
−
−
=
= −
I
I
0
0
, 4
, 3
,
, , 1
,
3,1 ,
2, 1
i j
i j j
i N
j N i
∑
∑
+
=
= −
= − +
I
I
0
0
*
,5
,
,
,
1, 1
N
i N
i N
i N
∑
=
= −
I
c r
т
12
N
–12
6
N
–6
,5
,5
,
,
, 1
,
2, 1 ,
* 1,
1
j
i j
i j
i j
i N
j N i
∑
∑
+
= +
= −
= − +
I
c r I
т
6
N
2
–8
N
+12
7,5
N
2
–
22,5
N
+15
, 1
,
N N N
∑
∑
=
I
I
0
0
, 1
, 2
, 5
,
, 1
, 1
2 ,
1,
1
i i
i
i i
i i
i
N
∑ ∑
∑
∑
+
+
= + +
= −
I I
I
I
0
27
N
–27
, 1
, 5
,
,
,
1,
1,
i j
j
i j
i
N j N
∑
∑
∑
= +
= − =
I I
I
T
0
9
N
–9
, 1
, 4
, 5
,
,
,
,
1,
2,
1,
1
i j
j
i j
i j
i
N
j i
N
∑
∑
∑
∑
= + +
= −
= + −
I I
I
I
т
0
9
N
2
–7
N
+18
,
1
N N
rr
rel
rel
j i
i
i j
j
i
j i
∑
≥
= =
=
∑ ∑
A
R I R
т
6
N
2
+6
N
4
N
2
+4
N
Всего для рекуррентного алгоритма
2
N
3
+18
N
2
–
–8
N
2,5
N
3
+19
N
2
+
+5,5
N
–19
Всего операций для рекуррентного алго-
ритма
4,5
N
3
+37
N
2
+243,5
N
–19
Алгоритм «косынка»
3
N
3
+24
N
2
–
–9
N
11
N
3
+105
N
2
–
–50
N
Алгоритм «косынка» всего вычислений
14
N
3
+129
N
2
–59
N
*
Умножение кососимметричных матриц выполняется по специальному алго-
ритму, учитывающему их структуру и обеспечивающему исключение избыточ-
ных вычислений.


