В.Е. Карасик, Е.Е. Мухина, В.М. Орлов
6
Применив методику, используемую в работе [3], получим выраже-
ние для пространственно-углового распределения яркости
L
(
r
,
α
,
z
),
где
r
=
l
— расстояние от оси лазерного пучка до точки наблюдения;
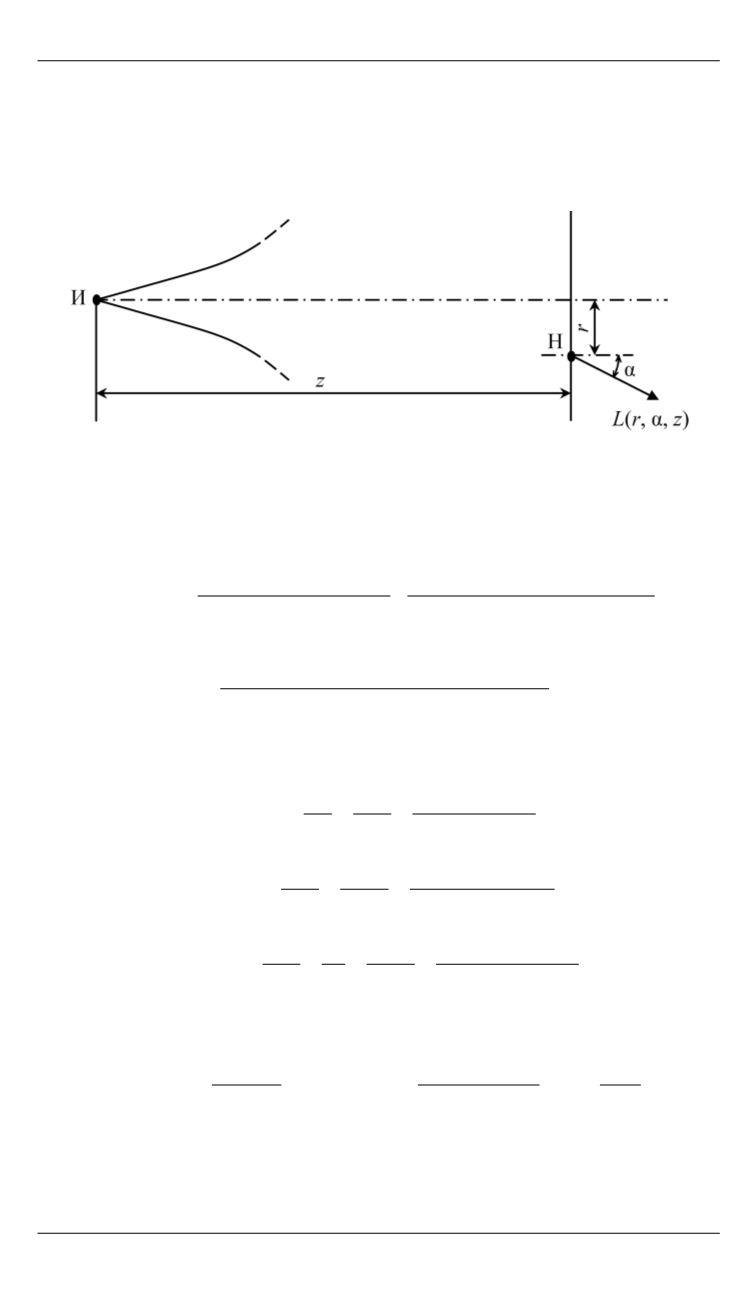
α
— угол между осью лазерного пучка и осью наблюдения (рис. 2).
Рис. 2.
Схема рассеяния в малоугловом приближении:
И — лазерный маяк; Н — наблюдатель
Яркость рассеянной компоненты светового поля имеет вид
[
]
0
р
2
2
2
0
1
0
exp (1 )
exp (
)
( , , )
16
( , )
( , )
( , )
P
z
x
L r z
a z x a z x a z x
π
Λε
− − Λ ε
−Λε
α =
×
π
−
−
∫
(
)
2
2
0
1
2
2
2
0
1
( , )
2 ( , )
( , )
exp
,
4 ( , ) ( , )
( , )
a z x r a z x r a z x dx
a z x a z x a z x
⎡
⎤
−
α −
α
×
⎢
⎥
−
⎢
⎥
⎣
⎦
(6)
где
2
2
2
и
0
6
6 (
)
( , )
;
4 4
4
z x
a z x
α μ Λε μ −
= + +
2
2
2 2 2
и
1
6
6 (
)
( , )
;
4 4
8
z
x
z x
a z x
α μ Λε μ −
= + +
2
2
2
2 3 3
и
и
2
6
6 (
)
( , )
.
4 4 4
12
z r
x
z x
a z x
α
μ Λε μ −
= + + +
Яркость нерассеянной (прямой) компоненты светового поля
( )
(
)
2 2 2
2
0
п
2 2 2
2
2
и и
и
и
( , , )
exp exp
exp
.
r z
P
L r z
z
r
r
⎡
⎤
− + α
⎛
⎞
−α
α =
−ε
⎢
⎥ ⎜
⎟
π α
α
⎣
⎦ ⎝
⎠
(7)
Суммарная яркость светового поля
п
р
( , , )
( , , )
( , , ).
L r z L r z L r z
α = α + α
(8)


