Необратимые процессы в квантовой телепортации
7
и
C
, получаем выражение для матрицы плотности частицы
B
, из ко-
торой, в свою очередь, с помощью (4) получаем энтропию на выходе
измерителя Боба (фактически это оказывается классическая энтропия
Шеннона). В общем случае она будет определяться углом поворота
и степенью декогеренции
p
. Очевидно, что при отсутствии декоге-
ренции она всегда равна нулю при любых углах поворота:
out
0,
0.
B
S p
Теперь последовательно рассмотрим различные модели декоге-
ренции. Энтропии выходного состояния при различных значениях
и
p
для квантового канала (7) представлены на рис. 2,
а
. Видно, что
энтропия всегда равна 0 не только для
p
= 0, но и на границах рас-
пределения по углу
:
0
и
.
При этих углах на вход теле-
портации поступают состояния 0 и 1 . Данные векторы не изменя-
ются под действием трансформации дефазирования (6). Таким обра-
зом, разрушение квантового канала через дефазирование не влияет
на передачу классического бита информации, закодированного через
состояния
0
и
1
.
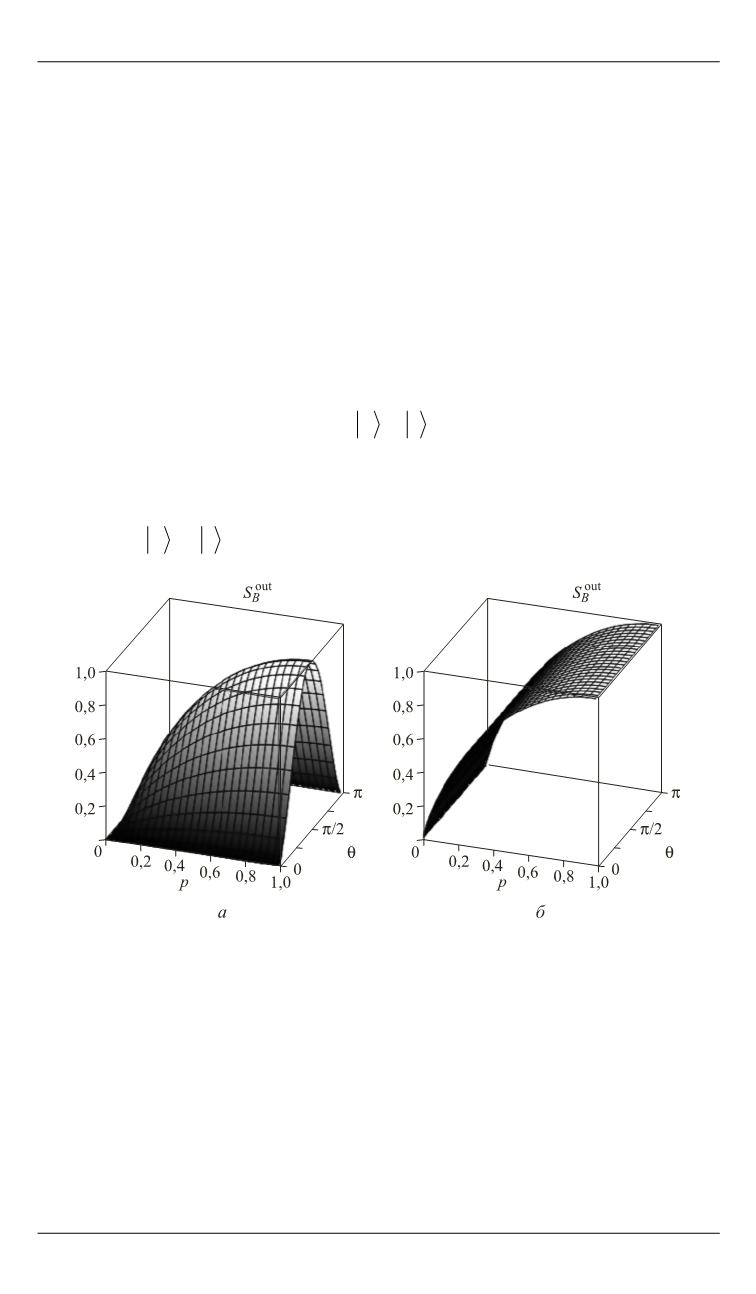
Рис. 2.
Зависимость энтропии выходного состояния от параметров
p
и
при
воздействии на квантовый канал дефазирования (
а
) и деполяризации (
б
)
В случае деполяризации (рис. 2,
б
) энтропия выходного сигнала
определяется лишь степенью декогеренции
p
и не зависит от входно-
го сигнала. Деполяризация разрушает все возможные корреляции так,
что невозможно получить выигрыш за счет выбора некоторого опти-
мального базиса для передачи информации.
Наибольший интерес представляет случай диссипации. Напомним,
что в зависимости от ее воздействия на частицы
С
или
B
получают раз-
личные матрицы плотности (11). Однако непосредственные вычисления


