Е.О. Киктенко, С.М. Коротаев
4
образований (2). В результате в идеальном случае у Боба должно ока-
заться состояние
cos 0 sin 1
2
2
B
B
B
. Теперь, чтобы убедиться
в успешности телепортации, Боб поворачивает свое состояние обрат-
но на угол
и в идеальном случае получает состояние 0
B
. Изме-
ряя свое состояние в базисе 0 , 1 , он должен со 100 %-ной
вероятностью получить состояние 0 (считаем, что детектор идеален).
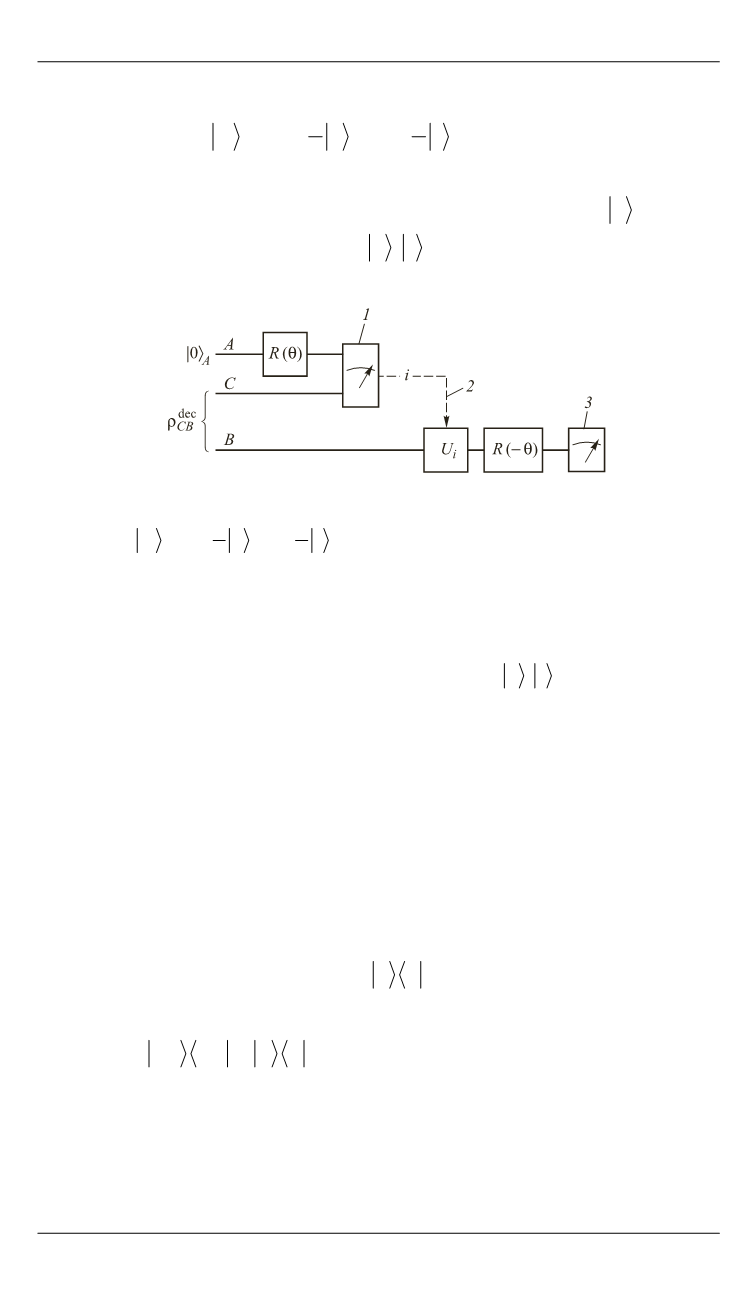
Рис. 1.
Схема к оценке точности телепортации произвольного
состояния
cos 0 sin 1
2
2
с использованием неидеального квантового
канала
dec
:
CB
,
R
R
— унитарные преобразования поворота;
i
U
— одно из унитарных
преобразований (2);
1
— совместное измерение в базисе Белла;
2
— классический
канал связи;
3
— измерение в базисе
0 , 1
В случае декогеренции квантового канала показания детектора
Боба будут иметь некоторый разброс, определяемый энтропией вы-
ходного состояния
out
B
S
. В рассматриваемых далее ситуациях декоге-
ренции выходное состояние
out
B
оказывается диагональным, и по-
этому энтропия фон Неймана (4) состояния
out
B
совпадает с энтропи-
ей Шеннона показаний детектора Боба.
С учетом измерения Боба схема, представленная на рис. 1, опи-
сывается преобразованием
out, dec
dec
†
1...4
0,1
0 0
,
ACB
ij
CB ij
A
i
j
(5)
где
4
;
ij
i
i
i
j j R U R
4
— единичная
матрица размерности 4
4.
Модели декогеренции.
Рассмотрим модели различных процессов
декогеренции, которые могут воздействовать на квантовый канал.
Можно выделить три основных варианта декогеренции: дефазирование,
деполяризацию и диссипацию. Каждый из них является необратимым


